(本小题满分13分)
在数列{ 中,
中,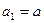 (
( 且
且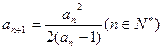
(1)求证 ;(2)求证
;(2)求证 ;
;
(3)若存在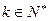 ,使得
,使得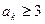 ,求证:
,求证:
(本小题满分13分)
已知曲线D: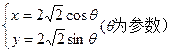 交
交 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率 的椭圆。
的椭圆。
(1)求椭圆的标准方程;
(2)设M是直线 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且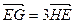 。试求此时弦PQ的长。
。试求此时弦PQ的长。
(本小题满分13分)
已知函数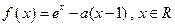 .
.
(1)若实数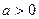 ,求函数
,求函数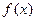 在
在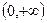 上的极值;
上的极值;
(2)记函数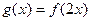 ,设函数
,设函数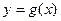 的图象C与
的图象C与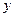 轴交于
轴交于 点,曲线C在
点,曲线C在 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为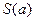 ,求当
,求当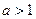 时
时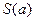 的最小值。
的最小值。
(本小题满分12分)
已知四边形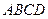 是边长为
是边长为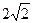 的正方形,
的正方形,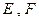 分别为
分别为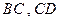 的中点,沿
的中点,沿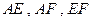 将
将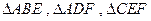 向同侧折叠且与平面
向同侧折叠且与平面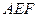 成直二面角,连接
成直二面角,连接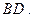
(1)求证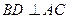 ;
;
(2)求平面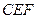 与平面
与平面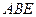 所成锐角的余弦值。
所成锐角的余弦值。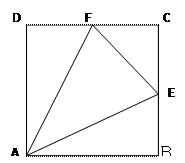

(本小题满分12分)
上海世博会于2010年5月1日正式开幕,按规定个人参观各场馆需预约,即进入园区后持门票当天预约,且一张门票每天最多预约六个场馆。考虑到实际情况(排队等待时间等),张华决定参观甲、乙、丙、丁四个场馆。假设甲、乙、丙、丁四个场馆预约成功的概率分别是 且它们相互独立互不影响。
且它们相互独立互不影响。
(1)求张华能成功预约甲、乙、丙、丁中两个场馆的概率;
(2)用 表示能成功预约场馆的个数,求随机变量
表示能成功预约场馆的个数,求随机变量 的分布列和数学期望。
的分布列和数学期望。