水利部门为加强防汛工作，决定对某水库大坝进行加固，大坝的横截面是梯形ABCD.如图所示，已知迎水坡面AB的长为16米，∠B=600，背水坡面CD的长为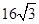
米，加固后大坝的横截面积为梯形ABED，CE的长为8米。
已知需加固的大坝长为150米，求需要填土石方多少立方米？
求加固后的大坝背水坡面DE的坡度。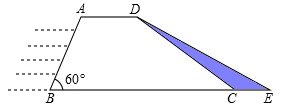
如图，点A、B、C、D在同一条直线上，BE∥DF，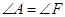
，
。
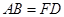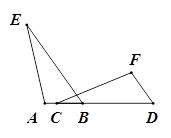
求证：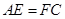
。
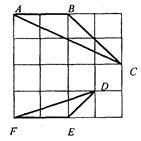
如图，在4×4的正方形网格中，△ABC和
△DEF的顶点都在边长为1的小正方形的顶点上．(1)填空：∠ABC=__________°，BC=__________；
(2)判断△ABC与△DEF是否相似，并证明你的结论．
如图，AB•AC=AD•AE，且∠1=∠2，求证：△ABC∽△AED．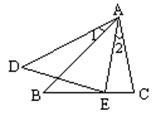
（1）计算：
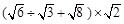． （2）解方程：
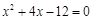
(14分)已知抛物线y＝ax2＋bx＋c(a≠0)经过A(－2，0)、B(0，1)两点，且对称轴是y轴．经过点C(0，2)的直线l与x轴平行，O为坐标原点，P、Q为抛物线y＝ax2＋bx＋c(a≠0)上的两动点．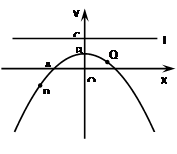
(1) 求抛物线的解析式；
(2) 以点P为圆心，PO为半径的圆记为⊙P，判断直线l与⊙P的位置关系，并证明你的结论；
(3) 设线段PQ＝9，G是PQ的中点，求点G到直线l距离的最小值．