问题背景
若矩形的周长为1，则可求出该矩形面积的最大值.我们可以设矩形的一边长为x，面积为s，则s与x的函数关系式为： 
，利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？
分析问题
若设该矩形的一边长为x，周长为y，则y与x的函数关系式为：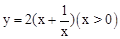
，问题就转化为研究该函数的最大（小）值了.
解决问题
借鉴我们已有的研究函数的经验，探索函数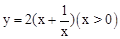的最大（小）值.
（1）实践操作：填写下表，并用描点法画出函数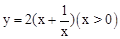的图象：
| x |
··· |
 |
 |
 |
1 |
2 |
3 |
4 |
··· |
| y |
|
|
|
|
|
|
|
|
|
（2）观察猜想：观察该函数的图象，猜想当x= 时，函数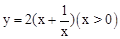有最 值（填
“大”或“小”），是 .
（3）推理论证：问题背景中提到，通过配方可求二次函数的最大值，请你尝试通过配方求函数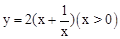的最大（小）值，以证明你的猜想. 〔提示：当
时，
〕
伟大的文学家、杰出的社会活动家高尔基说：“书籍，是人类进步的阶梯”，阅读使你增长知道，陶冶情操。李楠同学在课外阅读《三国演义》时，她将书翻到某一页，看完后往前翻了10页，然后她又往后翻了8页，这时她发现这三页的页码之和刚好是100，那么该书的这三页的页码分别是多少？
如图所示，在菱形ABCD中，BE⊥AD，BF⊥CD，E，F为垂足，AE=ED，求∠EBF的度数．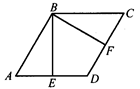
（1）如图（1），在△ABC中，∠ABC、∠ACB的平分线相交于点O，∠A=40°，求∠BOC的度数。
（2）如图（2），△DEF两个外角的平分线相交于点G，∠D=40°，求∠EGF的度数。
(3)由（1）、（2）可以发现∠BOC与∠EGF有怎样的数量关系？
设∠A=∠D=n°,∠BOC与∠EGF是否还具有这样的数量关系？
为什么？
阅读与理解：
（1）先阅读下面的解题过程：
分解因式：
解：方法（1）原式
方法（2）原式
再请你参考上面一种解法，对多项式进
行因式分解；
（2）阅读下面的解题过程：
已知
：，试求
与
的值。
解：由已知得：
因此得到：
所以只有当
并且
上式才能成立。
因而得：
并且
请你参考上面的解题方法解答下面的问题：
已知：
，试求
的值
若
的值