阅读与理解:
(1)先阅读下面的解题过程:
分解因式:
解:方法(1)原式



方法(2)原式



再请你参考上面一种解法,对多项式进 行因式分解;
行因式分解;
(2)阅读下面的解题过程:
已知 :,试求
:,试求 与
与 的值。
的值。
解:由已知得:
因此得到:
所以只有当 并且
并且 上式才能成立。
上式才能成立。
因而得: 并且
并且
请你参考上面的解题方法解答下面的问题:
已知: ,试求
,试求 的值
的值
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
(1)判断AE与⊙O的位置关系,并说明理由;
(2)当BC=4,AC=3CE时,求⊙O的半径.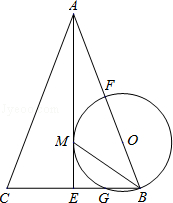
我们学习过:在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动叫做旋转,这个定点称为旋转中心,旋转的角度称为旋转角.
(1)如图(1),△ABC经过旋转得到△DEF.试用直尺和圆规作出旋转中心(保留作图痕迹,不写作法);
(2)如图(2),正方形ABCD中,E、F分别为CD、AD的中点,连接BE、CF,△BCE按逆时针方向旋转后得到△CDF,则旋转中心为(请在图中画出该点,标上字母,并回答),旋转的最小角度为.
体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明);
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
为了增强环境保护意识,6月5日“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:
| 组别 |
噪声声级分组 |
频数 |
频率 |
| 1 |
44.5﹣﹣59.5 |
4 |
0.1 |
| 2 |
59.5﹣﹣74.5 |
a |
0.2 |
| 3 |
74.5﹣﹣89.5 |
10 |
0.25 |
| 4 |
89.5﹣﹣104.5 |
b |
c |
| 5 |
104.5﹣119.5 |
6 |
0.15 |
| 合 计 |
40 |
1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a=,b=,c=;
(2)补充完整频数分布直方图;
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?