现有一个种植总面积为540m2的矩形塑料温棚,分垄间隔套种草莓和西红柿共24垄,种植的草莓或西红柿单种农作物的总垄数不低于10垄,又不超过14垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
| |
占地面积(m/垄) |
产量(千克/垄) |
利润(元/千克) |
| 西红柿 |
30 |
160 |
1.1 |
| 草莓 |
15 |
50 |
1.6 |
(1)若设草莓共种植了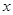 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
(2)在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
某校七、八年级各有10名同学参加市级数学竞赛,各参赛选手的成绩如下(单位:分)
七年级:89,92,92,92,93,95,95,96,98,98
八年级:88,93,93,93,94,94,95,95,97,98
整理得到如下统计表:
|
年级 |
最高分 |
平均分 |
众数 |
方差 |
|
七年级 |
98 |
94 |
|
7.6 |
|
八年级 |
98 |
94 |
93 |
|
根据以上信息,完成下列问题:
(1)填空: ;
(2)求表中 的值,并判断两个年级中哪个年级成绩更稳定;
(3)七年级两名最高分选手分别记为: , ,八年级第一、第二名选手分别记为: , ,现从这四人中,任意选取两人参加市级经验交流,请用树状图法或列表法求出这两人分别来自不同年级的概率.
如图,在平面直角坐标系中, 为等腰直角三角形, ,抛物线 经过 , 两点,其中点 , 的坐标分别为 , ,抛物线的顶点为点 .
(1)求抛物线的解析式;
(2)点 是直角三角形 斜边 上的一个动点(不与 , 重合),过点 作 轴的垂线,交抛物线于点 ,当线段 的长度最大时,求点 的坐标;
(3)在(2)的条件下,抛物线上是否存在一点 ,使 是以 为直角边的直角三角形?若存在,求出所有点 的坐标;若不存在,请说明理由.
如图, 是 的外接圆, 为直径, 的平分线交 于点 ,过点 的切线分别交 , 的延长线于 , ,连接 .
(1)求证: ;
(2)若 , ,求 的半径.

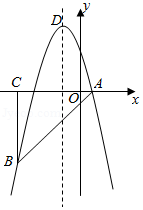
如图,在四边形 中, , 平分 , ,垂足为点 .
(1)求证:四边形 是菱形;
(2)若 , ,求四边形 的面积.
政府为了美化人民公园,计划对公园某区域进行改造,这项工程先由甲工程队施工10天完成了工程的 ,为了加快工程进度,乙工程队也加入施工,甲、乙两个工程队合作10天完成了剩余的工程,求乙工程队单独完成这项工程需要几天.