已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点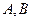 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存在直线 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
某商店投入38万元经销某种纪念品,经销期60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这一产品期间第 天的利润
天的利润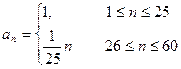 (单位:万元,
(单位:万元, ),记第
),记第 天的利润率
天的利润率 ,例如
,例如
(Ⅰ)求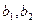 的值;
的值;
(Ⅱ)求第 天的利润率
天的利润率 ;
;
(Ⅲ)该商店在经销此纪品期间,哪一天的利润率最大?并求该天的利润率。
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,AD>BC,E,F分别为棱AB,PC的中点.
(I)求证:PE⊥BC;
|
(II)求证:EF//平面PAD.
某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出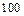 人的成绩作为样本.对高一年级的
人的成绩作为样本.对高一年级的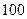 名学生的成绩进行统计,并按
名学生的成绩进行统计,并按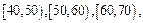
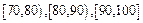 分组,得到成绩分布的频率分布直方图(如图).
分组,得到成绩分布的频率分布直方图(如图).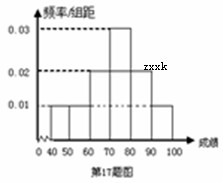
(Ⅰ)若规定60分以上(包括60分)为合格,计算高一年级这次知识竞赛的合格率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(Ⅲ)若高二年级这次知识竞赛的合格率为60%,由以上统计数据填写下面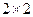 列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
列联表,并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系”。
| 高一 |
高二 |
合计 |
|
| 合格人数 |
|||
| 不合格人数 |
|||
| 合计 |
参考数据与公式:
由列联表中数据计算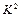 的公式
的公式 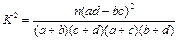
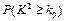 |
0.10 |
0.05 |
0.010 |
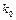 |
2.706 |
3.841 |
6.635 |
临界值表
(本小题满分12分)若函数 的图象与直线
的图象与直线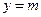 相切,相邻切点之间的距离为
相切,相邻切点之间的距离为 .
.
(Ⅰ)求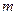 的值;
的值;
(Ⅱ)若点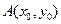 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标.
的坐标.