(本小题满分12分)
已知椭圆M的中心为坐标原点 ,且焦点在x轴上,若M的一个顶点恰好是抛物线 的焦点,M的离心率
的焦点,M的离心率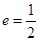 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线 ,交M于A,B两点。
,交M于A,B两点。
(1)求椭圆M的标准方程;
(2)设点N(t,0)是一个动点,且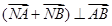 ,求实数t的取值范围。
,求实数t的取值范围。
(本小题满分12分)
从射击、乒乓球、跳水、田径四个大项的雅典奥运冠军中选出6名作“夺冠之路”的励志报告.
(1)若每个大项中至少选派一人,则名额分配有几种情况?
(2)若将6名冠军分配到5个院校中的4个院校作报告,每个院校至少一名冠军,则有多少种不同的分配方法?
(本小题满分10分)设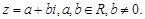 , 且
, 且 是实数,且
是实数,且 .
.
(1)求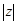 的值及
的值及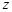 的实部的取值范围;
的实部的取值范围;
(2)设 ,求证:
,求证: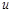 为纯虚数;
为纯虚数;
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列 的前
的前 项和为
项和为 ,且
,且 ,
,
(1)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(2)若 ,
, ,求证:数列
,求证:数列 为等比数列,并求出其通项公式;
为等比数列,并求出其通项公式;
(3)记 ,若对任意的
,若对任意的 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本题满分16分,第1小题4分,第2小题7分,第3小题5分)
如图,射线 所在的直线的方向向量分别为
所在的直线的方向向量分别为 ,
, ,点
,点 在
在 内,
内, 于
于 ,
, 于
于 ;
;
(1)若 ,
, ,求
,求 的值;
的值;
(2)若 ,
, 的面积为
的面积为 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数, 的中点为
的中点为 ,且
,且 ,当
,当 变化时,求动点
变化时,求动点 轨迹方程;
轨迹方程;
(本题满分14分,第1小题6分,第2小题8分)
已知函数 的反函数为
的反函数为
(1)若 ,求实数
,求实数 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间 内有解,求实数
内有解,求实数 的取值范围;
的取值范围;