已知集合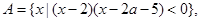 函数
函数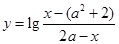 的定义域为集合B。 (1)若
的定义域为集合B。 (1)若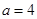 ,求集合
,求集合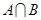 ;
;
(2)已知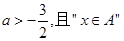 是“
是“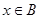 ”的充分不必要条件,求实数a的取值范围。
”的充分不必要条件,求实数a的取值范围。
写出下列命题的否命题及命题的否定形式,并判断真假:
(1)若m>0,则关于x的方程x2+x-m=0有实数根;
(2)若x、y都是奇数,则x+y是奇数;
(3)若abc=0,则a、b、c中至少有一个为零.
指出下列命题的真假:
(1)命题“不等式(x+2)2≤0没有实数解”;
(2)命题“1是偶数或奇数”;
(3)命题“ 属于集合Q,也属于集合R”;
属于集合Q,也属于集合R”;
(4)命题“A A
A B”.
B”.
写出下列命题的否定并判断真假.
(1)p:所有末位数字是0的整数都能被5整除;
(2)q: x≥0,x2>0;
x≥0,x2>0;
(3)r:存在一个三角形,它的内角和大于180°;
(4)t:某些梯形的对角线互相平分.
已知a>0,设命题p:函数y=ax在R上单调递减,q:不等式x+|x-2a|>1的解集为R,若p和q中有且只有一个命题为真命题,求a的取值范围.
已知p:|1-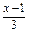 |≤2,q:x2-2x+1-m2≤0(m>0),且
|≤2,q:x2-2x+1-m2≤0(m>0),且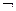 p是
p是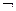 q的必要而不充分条件,求实数m的取值范围.
q的必要而不充分条件,求实数m的取值范围.