如图,在侧棱垂直于底面的三棱柱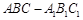 中,
中,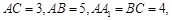 点
点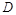 是
是 的中点.
的中点.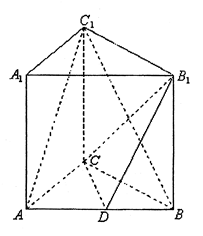
(1)求证: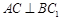 ;
;
(2)求证: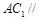 平面
平面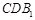 ;
;
(3)求三棱锥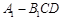 的体积.
的体积.
(本小题满分14分)设 ,函数
,函数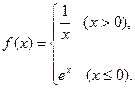 ,
, ,
,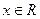 .
.
⑴当 时,求
时,求 的值域;
的值域;
⑵试讨论函数 的单调性.
的单调性.
(本小题满分12分)已知函数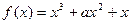 ,
,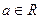 是常数,
是常数, .
.
⑴若 是曲线
是曲线 的一条切线,求
的一条切线,求 的值;
的值;
⑵ ,试证明
,试证明 ,使
,使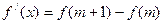 .
.
已知函数 ,
, 为函数
为函数 的导函数.
的导函数.
(Ⅰ)若数列 满足:
满足: ,
, (
(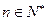 ),求数列
),求数列 的通项
的通项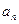 ;
;
(Ⅱ)若数列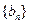 满足:
满足: ,
, (
(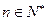 ).
).
ⅰ.当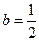 时,数列
时,数列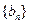 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列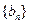 的通项
的通项 ;若不是,请说明理由;
;若不是,请说明理由;
ⅱ.当 时, 求证:
时, 求证: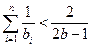 .
.
已知函数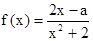 (x∈R)在区间[-1,1]上是增函数
(x∈R)在区间[-1,1]上是增函数
(Ⅰ)求实数a的值所组成的集合A
(Ⅱ)设关于x的方程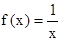 的两实数根为x1、x2.
的两实数根为x1、x2.
试问:是否存在实数m,使得不等式 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
(本小题满分14分)数列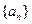 和数列
和数列 由下列条件确定:
由下列条件确定:
① ;
;
②当 时,
时,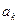 与
与 满足如下条件:当
满足如下条件:当 时,
时,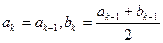 ;当
;当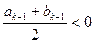 时,
时, 。
。
解答下列问题:
(Ⅰ)证明数列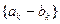 是等比数列;
是等比数列;
(Ⅱ)求数列 的前n项和为
的前n项和为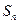 ;
;
(Ⅲ)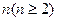 是满足
是满足 的最大整数时,用
的最大整数时,用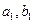 表示n的满足的条件。
表示n的满足的条件。