（本小题满分12分）如图，在三棱柱ABC－A1B1C1中，H是正方形AA1B1B的中心，AA1＝2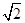
，C1H⊥平面AA1B1B，且C1H＝
.
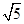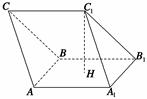
（1）求异面直线AC与A1B1所成角的余弦值；
（2）求二面角A－A1C1－B1的正弦值；
（3）设N为棱B1C1的中点，点M在平面AA1B1B内，且MN⊥平面A1B1C1，求线段BM的长．
（本小题满分12分）
已知数列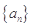
中，
，前项和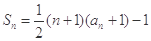
．
（1）求数列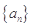的通项公式；
（2）设数列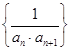
的前项和为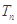
，是否存在实数
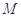，使得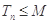
对一切正整数都成立？若存在，求出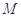的最小值；若不存在，请说明理由．
（本小题满分12分）
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在AB上，且OM∥AC.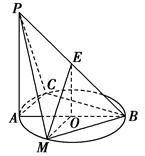
（1）求证：平面MOE∥平面PAC；
（2）求证：平面PAC⊥平面PCB；
（3）设二面角M－BP－C的大小为θ，求
的值．
（本小题满分12分）已知函数
的最大值为
．
（1）求常数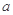
的值；
（2）求函数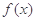
的单调递增区间；
（3）若将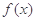的图象向左平移
个单位，得到函数
的图象，求函数在区间
上的最大值和最小值．
（本小题满分10分）设函数
.
（1）求函数
的最小值；
（2）若
,使得不等式
成立，求实数
的取值范围.
中，角A，B,C的对边分别是
且满足
，求
的值；