在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系. 已知点
轴的非负半轴为极轴建立极坐标系. 已知点 、
、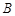 的极坐标分别为
的极坐标分别为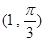 、
、 ,曲线
,曲线 的参数方程为
的参数方程为 为参数).
为参数).
(Ⅰ)求直线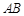 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线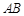 和曲线C只有一个交点,求
和曲线C只有一个交点,求 的值.
的值.
已知数列 中,
中,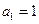 ,且
,且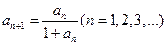 ,
,
(1)试归纳出这个数列的通项公式;(不用证明)
(2)设数列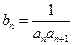 ,求数列
,求数列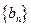 的前n项和
的前n项和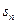 .
.
已知函数 ,若函数
,若函数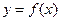 在
在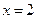 处有极值-6,求
处有极值-6,求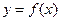 的单调递减区间;
的单调递减区间;
在直角坐标系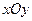 中,点P到两点
中,点P到两点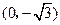 ,
, 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为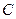 ,直线
,直线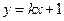 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若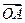
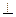
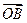 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|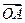 |>|
|>|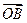 |
|
. (14分)
某分公司经销某种品牌产品,每件产品的成本为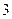 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交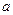 元(
元(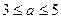 )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为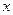 元(
元(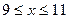 )时,一年的销售量为
)时,一年的销售量为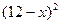 万件.
万件.
(1)求分公司一年的利润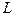 (万元)与每件产品的售价
(万元)与每件产品的售价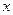 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润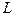 最大,并求出
最大,并求出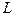 的最大值
的最大值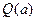 .
.
在四棱锥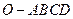 中,底面
中,底面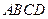 为菱形,
为菱形,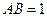 ,
,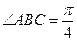 ,
,  ,
, 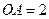 ,
,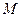 为
为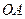 的中点,
的中点, 为
为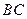 的中点
的中点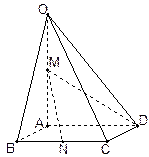
(Ⅰ)证明:直线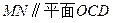
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。