. (14分)
某分公司经销某种品牌产品，每件产品的成本为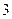
元，并且每件产品需向总公司交
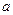元（
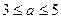）的管理费，预计当每件产品的售价为
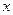元（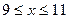
）时，一年的销售量为
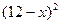万件.
（1）求分公司一年的利润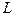
（万元）与每件产品的售价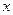的函数关系式；
（2）当每件产品的售价为多少元时，分公司一年的利润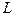最大，并求出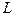的最大值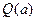
.
如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，
是AC的中点，已知
，
.
（1）求证：OD//平面VBC；
（2）求证：AC⊥平面VOD；
（3）求棱锥
的体积.
已知某山区小学有100名四年级学生，将全体四年级学生随机按00～99编号，并且按编号顺序平均分成10组．现要从中抽取10名学生，各组内抽取的编号按依次增加10进行系统抽样.
（1）若抽出的一个号码为22，则此号码所在的组数是多少？据此写出所有被抽出学生的号码；
（2）分别统计这10名学生的数学成绩，获得成绩数据的茎叶图如图4所示，求该样本的方差；
（3）在（2）的条件下，从这10名学生中随机抽取两名成绩不低于73分的学生，求被抽取到的两名学生的成绩之和不小于154分的概率．
在DABC中，角A、B、C的对边分别为a、b、c，且角A、B都是锐角，a=6，b=5，
.
（1） 求
和
的值；
（2） 设函数
，求
的值.
设函数
.
（1）若函数
在区间（-2，0）内恰有两个零点，求a的取值范围；
（2）当a=1时，求函数在区间[t，t+3]上的最大值.
设双曲线C：
（a>0，b>0）的一个焦点坐标为（
，0），离心率
， A、B是双曲线上的两点，AB的中点M（1，2）.
（1）求双曲线C的方程；
（2）求直线AB方程；
（3）如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D四点是否共圆？为什么？