如图，已知：直线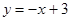
交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点.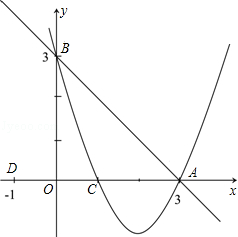
（1）求抛物线的解析式;
（2）若点D的坐标为（-1，0），在直线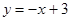上有一点P,使ΔABO与ΔADP相似，求出点P的坐标；
（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使ΔADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．
(本题满分8分)
为响应市政府“创建国家森林城市”的号召，某小区计划购进A、B两种树苗共17棵，已知A种树苗每棵80元，B种树苗每棵60元．
（1）若购进A、B两种树苗刚好用去1220元，问购进A、B两种树苗各多少棵？
（2）若购买的A种树苗的数量大于B种树苗的数量，请你给出一种费用最省的方案．
(本题满分6分)
手工课上，小明准备做一个形状是菱形的风筝，这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位：cm2)随其中一条对角线的长x(单位：cm)的变化而变化．
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
(2)当x是多少时，菱形风筝面积S最大?最大面积是多少?
参考公式：当x=-
时，二次函数y=ax2+bx+c(a≠0)有最小（大）值
(本题满分6分)
已知：如图，点F，C在BD 上，
， 
，
.
求证：
.
(本题满分6分)
在平面直角坐标系中，△ABC的位置如图所示，请解答下列问题：
（1）将△ABC向下平移3个单位长度，得到△A
BC，画出平移后的△ABC；（2）将△ABC绕点O旋转180°，得到△A
BC，画出旋转后的△ABC；
(本题满分6分)
先化简，再求代数式
的值，其中x= 
cos300+