24.(15)如图，MNP 为整直面内一固定轨道，其圆弧段MN与水平段NP相切于N、P端固定一竖直挡板。M相对于N的高度为h，NP长度为s.一木块自M端从静止开始沿轨道下滑，与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计，物块与NP段轨道间的滑动摩擦因数为μ，求物块停止的地方与N点距离的可能值。
长度为L的细线下挂一个质量为m的小球，小球半径忽略不计，现用一个水平力F拉小球使悬线偏离竖直方向θ角并保持静止状态，如图所示，撤掉F后，小球从静止开始运动到最低点时，求：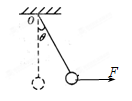
（1）小球的速度大小
（2）绳子拉力为多少？
将一个小球以
的速度沿水平方向抛出，小球经过
的时间落地。不计空气阻力作用。求：
（1）抛出点与落地点在竖直方向的高度差；
（2）小球落地时的速度大小
（3）以地面为零势能面，离地多高时动能是势能的3倍。
一列简谐横波在x轴上传播，在t1＝0和t2＝0.5 s两时刻的波形分别如图中的实线和虚线所示，求：
(1)周期
(2)波速
(3)若波速为92 m/s，求波的传播方向．
发电机输出功率为100 kW，输出电压是250 V，用户需要的电压是220 V，输电线电阻为10 Ω.若输电线中因发热而损失的功率为输送功率的4%，试求：
(1)用户得到的电功率是多少
(2)在输电线路中设置的升、降压变压器原副线圈的匝数比
有n=10匝的矩形线圈，每匝都是长50cm，宽20cm，线圈总电阻10Ω，在B=2T的匀强磁场中以角速度ω=50rad／s旋转.线圈与R=40Ω的外电阻连接，图中的电流表、电压表的接入不影响原电路.求：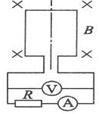
(1)流过电阻电流的瞬时表达式(从中性面开始计时)
(2)电流表、电压表的读数
(3)电路中1min内产生的热量
(4)从图示位置开始计时转过90度的过程中流过安培表的电量。