设 和
和 是函数
是函数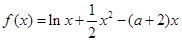 的两个极值点,其中
的两个极值点,其中 ,
, .
.
(1)若曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴,求实数
轴,求实数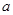 的值;
的值;
(2)求 的取值范围;
的取值范围;
(3)若 ,求
,求 的最大值(
的最大值( 是自然对数的底数).
是自然对数的底数).
已知函数 是定义在
是定义在 上的奇函数.当
上的奇函数.当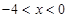 时,
时, ,且图象过点
,且图象过点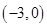 与点
与点 .
.
(Ⅰ)求实数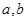 的值,并求函数
的值,并求函数 的解析式;
的解析式;
(Ⅱ)若关于 的方程
的方程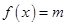 有两个不同的实数解,请写出实数
有两个不同的实数解,请写出实数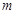 的取值范围;
的取值范围;
(Ⅲ)解关于 的不等式
的不等式 ,写出解集.
,写出解集.
用0,1,2,3,4这五个数字组成无重复数字的自然数。
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数。
已知数列 的前
的前 项和
项和 满足:
满足: ,
, 为常数,且
为常数,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,设
,设 ,且数列
,且数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知数列 的各项均为正整数,对于任意n∈N*,都有
的各项均为正整数,对于任意n∈N*,都有 成立,且
成立,且 .
.
(1)求 ,
, 的值;
的值;
(2)猜想数列 的通项公式,并给出证明.
的通项公式,并给出证明.