( 本小题满分12分)
已知点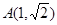 是离心率为
是离心率为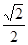 的椭圆
的椭圆 :
: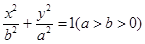 上的一点.斜率为
上的一点.斜率为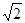 的直线
的直线 交椭圆
交椭圆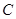 于
于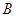 、
、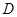 两点,且
两点,且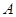 、
、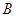 、
、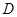 三点不重合.
三点不重合.
(Ⅰ)求椭圆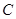 的方程;
的方程;
(Ⅱ) 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
(Ⅲ)求证:直线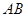 、
、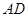 的斜率之和为定值.
的斜率之和为定值.
如图1,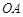 、
、 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段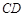 和曲线段
和曲线段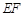 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥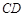 上某点
上某点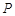 分别修建与
分别修建与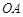 、
、 平行的栈桥
平行的栈桥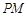 、
、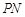 ,且以
,且以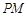 、
、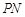 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台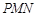 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段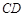 的方程是
的方程是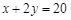
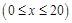 ,曲线段
,曲线段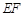 的方程是
的方程是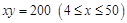 ,设点
,设点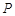 的坐标为
的坐标为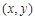 ,记
,记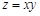 (题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(1)求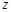 的取值范围;
的取值范围;
(2)试写出三角形观光平台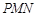 面积
面积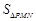 关于
关于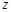 的函数解析式,并求出该面积的最小值.
的函数解析式,并求出该面积的最小值.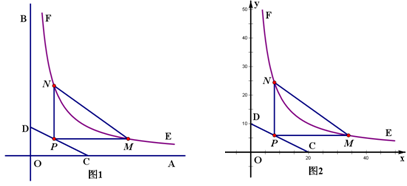
在所有棱长都相等的斜三棱柱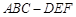 中,已知
中,已知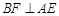 ,
,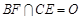 ,且
,且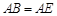 ,连接
,连接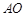 .
.
(1)求证: 平面
平面 ;
;
(2)求证:四边形 为正方形.
为正方形.
设函数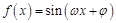 ,其中
,其中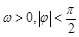 ,若
,若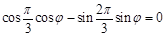 ,且图象的一条对称轴离一个对称中心的最近距离是
,且图象的一条对称轴离一个对称中心的最近距离是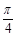 .
.
(1)求函数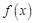 的解析式;
的解析式;
(2)若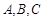 是
是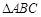 的三个内角,且
的三个内角,且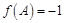 ,求
,求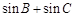 的取值范围
的取值范围
把函数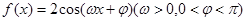 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移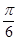 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2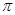 的奇函数
的奇函数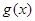 .
.
(1) 求 的值;
的值;
(2)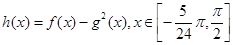 的单调区间和最值.
的单调区间和最值.
已知向量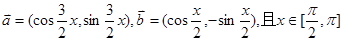 ,求:
,求:
(1)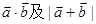 ;
;
(2)若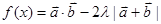 的最小值是
的最小值是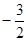 ,求实数
,求实数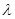 的值.
的值.