(本小题满分14分)(注意:在试题卷上作答无效)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为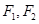 ,若以
,若以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过椭圆上一点
,过椭圆上一点 作此圆的切线,切点为
作此圆的切线,切点为 ,且
,且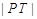 的最小值不小于为
的最小值不小于为 .
.
(1)求椭圆的离心率 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为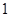 ,圆
,圆 与
与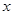 轴的右交点为
轴的右交点为 ,过点
,过点 作斜率为
作斜率为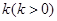 的直线
的直线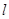 与椭圆相交于
与椭圆相交于 两点,若
两点,若 ,求直线
,求直线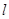 被圆
被圆 截得的弦长
截得的弦长 的最大值.
的最大值.
已知半径为5的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线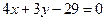 相切.
相切.
(1)求圆的方程;
(2)设直线 与圆相交于
与圆相交于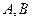 两点,求实数
两点,求实数 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数 ,使得过点
,使得过点 的直线
的直线 垂直平分弦
垂直平分弦 ?
?
存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
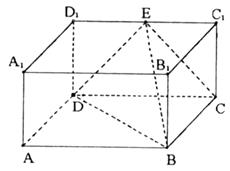
在长方体ABCD— 中,AB=2,
中,AB=2,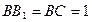 ,E为
,E为 的中点,连结ED,EC,EB和DB,
的中点,连结ED,EC,EB和DB,
(1)求证:平面EDB⊥平面EBC;
(2)求二面角E-DB-C的正切值.
 |
在中国轻纺城批发市场,季节性服装当季节即将来临时,价格呈上升趋势. 设某服装开始时定价为 10 元,并且每周(7 天)涨价 2 元,5 周后开始保持 20 元的平稳销售;10 周后当季节即将过去时,平均每周降价 2 元,直到 16 周末,该服装已不再销售.
(1)试建立价格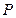 与周次
与周次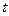 之间的函数关系;
之间的函数关系;
(2)若此服装每件进价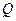 与周次
与周次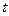 之间的关系式
之间的关系式 ,
,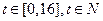 ,问该服装第几周每件销售利润最大?
,问该服装第几周每件销售利润最大?
已知函数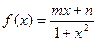 是定义在
是定义在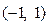 上的奇函数,且
上的奇函数,且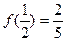
(1)求实数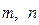 的值
的值
(2)用定义证明 在
在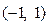 上是增函数
上是增函数
(3)解关于 的不等式
的不等式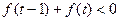
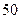
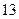
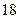

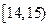
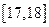
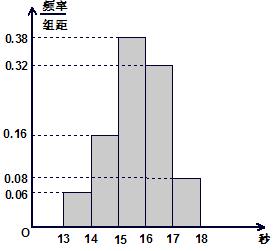
(Ⅰ)若成绩大于或等于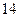 秒且小于
秒且小于 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于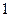 的概率。
的概率。