(本小题满分12分)
已知函数 ,函数
,函数 (
( ,且
,且 )
)
(Ⅰ)求函数 的定义域
的定义域
(Ⅱ)求使函数 的值为正数的
的值为正数的 的取值范围
的取值范围
16.(本小题满分12分)
已知向量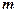
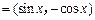 ,
,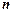
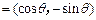 ,其中
,其中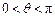 .函数
.函数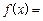
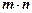 在
在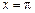 处取最小值.
处取最小值.
(Ⅰ)求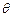 的值;
的值;
(Ⅱ)设 ,
,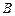 ,
,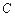 为
为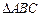 的三个内角,若
的三个内角,若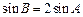 ,
,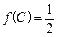 ,求
,求 .
.
21.(本小题满分14分)
设 是数列
是数列 的前
的前 项和,且
项和,且 是
是 和
和 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)当 (
( 均为正整数)时,求
均为正整数)时,求 和
和 的所有可能的乘积
的所有可能的乘积 之和
之和 ;
;
(3)设 ,求证:
,求证: .
.
20.(本小题满分14分)
已知抛物线 :
: 的焦点为
的焦点为 ,过点
,过点 作直线
作直线 交抛物线
交抛物线 于
于 、
、 两点;椭圆
两点;椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,点
轴上,点 是它的一个顶点,且其离心率
是它的一个顶点,且其离心率 .
.
(1)求椭圆 的方程;
的方程;
(2)经过 、
、 两点分别作抛物线
两点分别作抛物线 的切线
的切线 、
、 ,切线
,切线 与
与 相交于点
相交于点 .证明:
.证明: ;
;
(3)椭圆 上是否存在一点
上是否存在一点 ,经过点
,经过点 作抛物线
作抛物线 的两条切线
的两条切线 、
、 (
( 、
、 为切点),使得直线
为切点),使得直线 过点
过点 ?若存在,求出抛物线
?若存在,求出抛物线 与切线
与切线 、
、 所围成图形的面积;若不存在,试说明理由.
所围成图形的面积;若不存在,试说明理由.
 |
19.(本小题满分14分)
设函数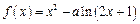 (
( ,
,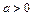 ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有最小值,指出其取得最小值时
是否有最小值?若有最小值,指出其取得最小值时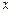 的值,并证明你的结论.
的值,并证明你的结论.
18.(本小题满分14分)
如图5,四边形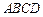 是圆柱
是圆柱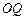 的轴截面,点
的轴截面,点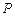 在圆柱
在圆柱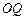 的底面圆周上,
的底面圆周上,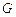 是
是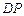 的中点,圆柱
的中点,圆柱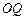 的底面圆的半径
的底面圆的半径 ,侧面积为
,侧面积为 ,
, .
.
(1)求证: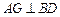 ;
;
(2)求二面角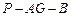 的平面角的余弦值.
的平面角的余弦值.