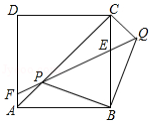
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°.点E为底AD上一点,将△ABE沿直线BE折叠,点A落在梯形对角线BD上的G处,EG的延长线交直线BC于点F.
(1)点E可以是AD的中点吗?为什么?
(2)求证:△ABG∽△BFE;
(3)设AD=a,AB=b,BC=c
①当四边形EFCD为平行四边形时,求a,b,c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.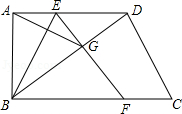
某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证: ;
(2)若 ,试判断四边形 的形状,并证明你的结论.

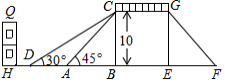
如图是某市一座人行天桥的示意图,天桥离地面的高 是10米,坡面 的倾斜角 ,在距 点10米处有一建筑物 .为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面 的倾斜角 ,若新坡面下 处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据: ,
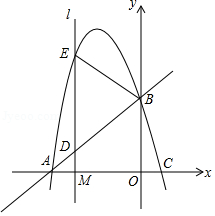
如图,抛物线 , 、 为常数)与 轴交于 、 两点,与 轴交于 点,直线 的函数关系式为 .
(1)求该抛物线的函数关系式与 点坐标;
(2)已知点 是线段 上的一个动点,过点 作 轴的垂线 分别与直线 和抛物线交于 、 两点,当 为何值时, 恰好是以 为底边的等腰三角形?
(3)在(2)问条件下,当 恰好是以 为底边的等腰三角形时,动点 相应位置记为点 ,将 绕原点 顺时针旋转得到 (旋转角在 到 之间);
.探究:线段 上是否存在定点 不与 、 重合),无论 如何旋转, 始终保持不变.若存在,试求出 点坐标;若不存在,请说明理由;
.试求出此旋转过程中, 的最小值.
边长为 的正方形 中, 是对角线 上的一个动点(点 与 、 不重合),连接 ,将 绕点 顺时针旋转 到 ,连接 , 与 交于点 , 延长线与 (或 延长线)交于点 .
(1)连接 ,证明: ;
(2)设 , ,试写出 关于 的函数关系式,并求当 为何值时, ;
(3)猜想 与 的数量关系,并证明你的结论.