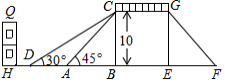
如图是某市一座人行天桥的示意图,天桥离地面的高 是10米,坡面 的倾斜角 ,在距 点10米处有一建筑物 .为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面 的倾斜角 ,若新坡面下 处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据: ,
甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两人的速度各是多少?
(2)求出甲距 地的路程
地的路程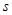 与行驶时间
与行驶时间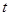 之间的函数关系式.
之间的函数关系式.
(3)在什么时间段内乙比甲离 地更近?
地更近?
如图所示,已知直线y=kx-2经过M 点,求此直线与x轴交点坐标和直线与两坐标轴围成三角形的面积.
在平面直角坐标系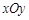 中,对于任意两点
中,对于任意两点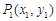 与
与 的“非常距离”,给出如下定义:
的“非常距离”,给出如下定义:
若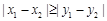 ,则点
,则点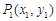 与点
与点 的非常距离为
的非常距离为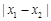 ;
;
若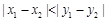 ,则点
,则点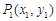 与点
与点 的非常距离为
的非常距离为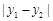 ;
;
例如:点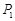 (1,2),点
(1,2),点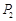 (3,5),因为
(3,5),因为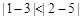 ,所以点
,所以点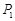 与点
与点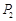 的“非常距离”为
的“非常距离”为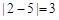 ,也就是图1中线段
,也就是图1中线段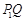 与线段
与线段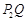 长度的较大值(点Q为垂直于y轴的直线
长度的较大值(点Q为垂直于y轴的直线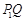 与垂直于x轴的直线
与垂直于x轴的直线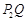 的交点).
的交点).
(1)已知点A(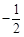 ,0),B为y轴上的一个动点,
,0),B为y轴上的一个动点,
①若点A与点B的“非常距离”为2,写出满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值.
(2)已知C是直线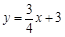 上的一个动点,
上的一个动点,
①如图2,点D的坐标是(0,1),求点C与点D的“非常距离”的最小值及相应的点C的坐标;
②如图3,E是以原点O为圆心,1为半径的圆上的一个动点,求点C与点E的“非常距离”的最小值及相应点E和点C的坐标.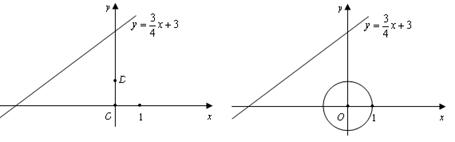
如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB=cm;当t=6时,AB=cm;
(2)问点A出发后多少秒两圆相切?
高致病性禽流感是比SARS传染速度更快的传染病,为了防止禽流感蔓延,政府规定离疫点3km范围内为扑杀区;离疫点3km—5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内大约有多少千米?( =1.732,
=1.732,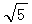 =2.236,结果精确到0.01km.)
=2.236,结果精确到0.01km.)