张勤同学的父母在外打工,家中只有年迈多病的奶奶.星期天早上,李老师从家中出发步行前往张勤家家访.6分钟后,张勤从家出发骑车到相距1200米的药店给奶奶买药,停留14分钟后以相同的速度按原路返回,结果与李老师同时到家.张勤家、李老师家、药店都在东西方向笔直大路上,且药店在张勤家与李老师家之间.在此过程中设李老师出发t(0≤t≤32)分钟后师生二人离张勤家的距离分别为S1、S2.S与t之间的函数关系如图所示,请你解答下列问题:
(1)李老师步行的速度为 ;
(2)求S2与t之间的函数关系式,并在如图所示的直角坐标系中画出其函数图象;
(3)张勤出发多长时间后在途中与李老师相遇?
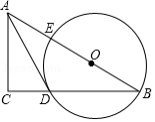
如图,在 中,点 在斜边 上,以 为圆心, 为半径作圆,分别与 , 相交于点 , ,连接 .已知 .
(1)求证: 是 的切线.
(2)若 , ,求 的半径.
为了解朝阳社区 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
已知, 中, , 是 边上一点,作 ,分别交边 , 于点 , .
(1)若 (如图 ,求证: .
(2)若 ,过点 作 ,交 (或 的延长线)于点 .试猜想:线段 , 和 之间的数量关系,并就 情形(如图 说明理由.
(3)若点 与 重合(如图 , ,且 .
①求 的度数;
②设 , , ,试证明: .

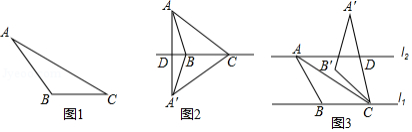
我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)概念理解:
如图1,在 中, , , ,试判断 是否是”等高底”三角形,请说明理由.
(2)问题探究:
如图2, 是“等高底”三角形, 是”等底”,作 关于 所在直线的对称图形得到△ ,连接 交直线 于点 .若点 是△ 的重心,求 的值.
(3)应用拓展:
如图3,已知 , 与 之间的距离为2.“等高底” 的“等底” 在直线 上,点 在直线 上,有一边的长是 的 倍.将 绕点 按顺时针方向旋转 得到△ , 所在直线交 于点 .求 的值.
已知,点 为二次函数 图象的顶点,直线 分别交 轴正半轴, 轴于点 , .
(1)判断顶点 是否在直线 上,并说明理由.
(2)如图1,若二次函数图象也经过点 , ,且 ,根据图象,写出 的取值范围.
(3)如图2,点 坐标为 ,点 在 内,若点 , , , 都在二次函数图象上,试比较 与 的大小.
