如图，在平面直角坐标系中，矩形OABC四个顶点的坐标分别为O(0，0)，A(0，3)，B(6，3)，C(6，0)，抛物线
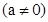过点A。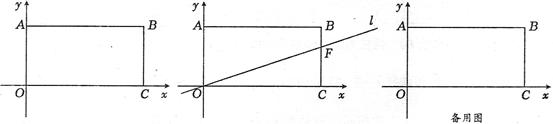
(1)(2分)求c的值； ．
(2)(6分)若a＝－l，且抛物线与矩形有且只有三个交点A、D、E，求△ADE的面积S的最大值；
(3)(6分)若抛物线与矩形有且只有三个交点A、M、N，线段MN的垂直平分线l过点O，交线段BC于点
F。当BF＝1时，求抛物线的解析式．
（本题10分）已知如图，在平面直角坐标系中，A（-1，-3），OB=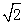
，OB与x轴所夹锐角是45°．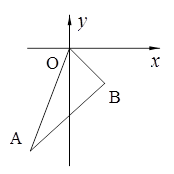
（1）求B点坐标；
（2）判断△ABO的形状；
（3）求△ABO最长边上的中线长．
（本题10分）将长为2.5米的梯子AC斜靠在墙上，梯子的底部离墙的底端1.5米（即图中BC的长）．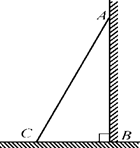
（1）求梯子的顶端与地面的距离；
（2）若梯子顶端A下滑1.3米，那么梯子底端C向左移动了多少米？
（本题10分）如图，在等边三角形ABC中，点D，E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．
（1）求∠F的度数；
（2）若CD=2，求DF的长．
（本题10分）如图，在平面直角坐标系xOy中，点A（−2，10），点B（6，10）．
（1）只用直尺（没有刻度）和圆规，求作一个点P，使点P同时满足下列两个条件：
①点P到A，B两点的距离相等；②点P到两坐标轴的距离相等．（要求保留作图痕迹，不必写出作法）
（2）求出（1）中点P的坐标．
（本题10分）已知：等腰三角形的周长为80．
（1）写出底边长y与腰长x的函数表达式；
（2）当腰长为30时，底边长为多少？
（3）当底边长为8时，腰长为多少？