某商场购进一批L型服装(数量足够多),进价为40元/件,以60元/件销售,每天销售20件。根据市场调研,若每件每降1元,则每天销售数量比原来多3件。现商场决定对L型服装开展降价促销活动,每件降价x元(x为正整数)。在促销期间,商场要想每天获得最大销售利润,每件降价多少元?每天最大销售毛利润为多少?(注:每件服装销售毛利润指每件服装的销售价与进货价的差)
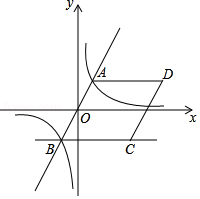
如图,反比例函数 的图象与正比例函数 的图象相交于 、 两点,点 在第四象限, 轴.
(1)求 的值;
(2)以 、 为边作菱形 ,求 点坐标.
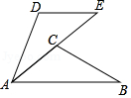
如图, , , , .
(1)求 的度数;
(2)若 ,求证: .
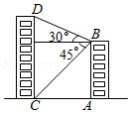
如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房 的楼顶,测量对面的乙栋楼房 的高度.已知甲栋楼房 与乙栋楼房 的水平距离 米,小丽在甲栋楼房顶部 点,测得乙栋楼房顶部 点的仰角是 ,底部 点的俯角是 ,求乙栋楼房 的高度(结果保留根号).
先化简,再求值: ,其中 .
如图1,抛物线 经过点 ,顶点为 ,对称轴 与 轴相交于点 , 为线段 的中点.
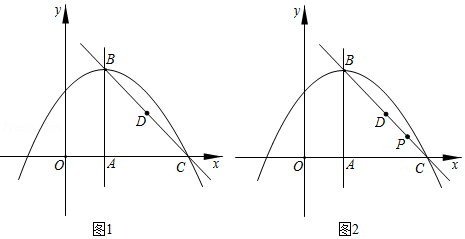
(1)求抛物线的解析式;
(2) 为线段 上任意一点, 为 轴上一动点,连接 ,以点 为中心,将 逆时针旋转 ,记点 的对应点为 ,点 的对应点为 .当直线 与抛物线 只有一个交点时,求点 的坐标.
(3) 在(2)的旋转变换下,若 (如图 .
①求证: .
②当点 在(1)所求的抛物线上时,求线段 的长.