.(本小题满分13分)
已知数列 是各项均不为
是各项均不为 的等差数列,公差为
的等差数列,公差为 ,
, 为其前
为其前 项和.向量
项和.向量 、
、 满足
满足 ,
, .数列
.数列 满足
满足 ,
, 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求 、
、 和
和 ;
;
(Ⅱ)若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
已知f(x)=lg(x+1),g(x)=2lg(2x+t),(t∈R是参数).
(1)当t=–1时,解不等式f(x)≤g(x);
(2)如果x∈[0,1]时,f(x)≤g(x)恒成立,求参数t的取值范围.
已知函数 (a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值
(a,c∈R,a>0,b是自然数)是奇函数,f(x)有最大值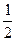 ,且f(1)>
,且f(1)>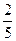 .
.
(1)求函数f(x)的解析式;
(2)是否存在直线l与y=f(x)的图象交于P、Q两点,并且使得P、Q两点关于点(1,0)对称,若存在,求出直线l的方程,若不存在,说明理由.
对任意函数f(x), x∈D,可按图示构造一个数列发生器,其工作原理如下:
①输入数据x0∈D,经数列发生器输出x1=f(x0);
②若x1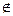 D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.
现定义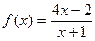
(1)若输入x0=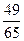 ,则由数列发生器产生数列{xn},请写出{xn}的所有项;
,则由数列发生器产生数列{xn},请写出{xn}的所有项;
(2)若要数列发生器产生一个无穷的常数列,试求输入的初始数据x0的值;
(3)若输入x0时,产生的无穷数列{xn},满足对任意正整数n均有xn<xn+1;求x0的取值范围.
设椭圆C1的方程为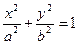 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=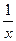 ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式.
把一个长、宽、高分别为25 cm、20 cm、5 cm的长方体木盒从一个正方形窗口穿过,那么正方形窗口的边长至少应为多少?