已知f(x)=lg(x+1),g(x)=2lg(2x+t),(t∈R是参数).
(1)当t=–1时,解不等式f(x)≤g(x);
(2)如果x∈[0,1]时,f(x)≤g(x)恒成立,求参数t的取值范围.
已知函数f(x)=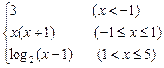
(1)讨论f(x)在点x=-1,0,1处的连续性;
(2)求f(x)的连续区间。
求证:方程x=asinx+b(a>0,b>0)至少有一个正根,且它不大于a+b.
已知函数f(x)=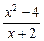 ,
,
(1)求f(x)的定义域,并作出函数的图像;
(2)求f(x)的不连续点x0;
(3)对f(x)补充定义,使其是R上的连续函数.
袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是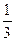 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
(i)求恰好摸5次停止的概率;
(ii)记5次之内(含5次)摸到红球的次数为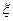 ,求随机变量
,求随机变量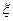 的分布率及数学期望E
的分布率及数学期望E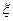 .
.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是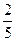 ,求p的值.
,求p的值.
设一部机器在一天内发生故障的概率为0 2,机器发生故障时全天停止工作
2,机器发生故障时全天停止工作 若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?
若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?