(本小题满分12分)
已知椭圆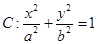
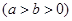 的离心率为
的离心率为 ,直线
,直线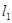 经过椭圆的上顶点
经过椭圆的上顶点 和右顶点
和右顶点 ,并且和圆
,并且和圆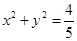 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设直线
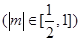 与椭圆
与椭圆 相交于
相交于 ,
,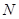 两点,以线段
两点,以线段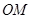 ,
, 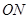 为邻边作平行四边行
为邻边作平行四边行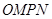 ,其中顶点
,其中顶点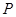 在椭圆
在椭圆 上,
上,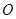 为坐标原点,求
为坐标原点,求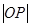 的取值范围.
的取值范围.
(满分12分)设函数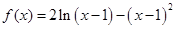 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(II)若关于 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数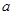 的取值范围.
的取值范围.
(满分12分)已知椭圆
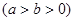 的一个顶点为B
的一个顶点为B ,离心率
,离心率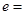
 ,
,
直线l交椭圆于M、N两点.
(Ⅰ)求椭圆的标准方程;
(II)如果ΔBMN的重心恰好为椭圆的右焦点F,求直线 的方程.
的方程.
(满分12分)如右图,在正三棱柱ABC—A1B1C1中,AA1=AB,D是AC的中点。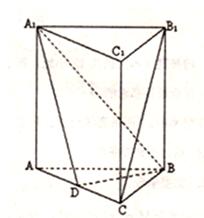
(Ⅰ)求证:B1C//平面A1BD;
(Ⅰ)求二面角A—A1B—D的余弦值。
(满分12分)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(II)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(满分12分)设数列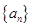 的前
的前 项和为
项和为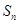 .已知
.已知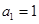 ,
,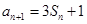 ,
,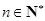 。
。
(Ⅰ)求数列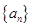 的通项公式;
的通项公式;
(Ⅱ)记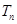 为数列
为数列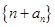 的前
的前 项和,求
项和,求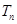 ;
;