(本小题满分12分)已知函数 ,若存在
,若存在 恒成立,则称
恒成立,则称 的一个“下界函数”.
的一个“下界函数”.
(I)如果函数 的一个“下界函数”,求实数t的取值范围(II)设函数
的一个“下界函数”,求实数t的取值范围(II)设函数 ,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
(本小题满分12分)已知数列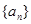 的前n项和为
的前n项和为 等差数列
等差数列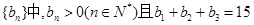 ,又
,又 成等比数列.
成等比数列.
(I)求数列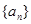 、
、 的通项公式;
的通项公式;
(II)求数列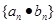 的前n项和
的前n项和 .
.
(本小题满分12分)从2003年开始,我国就通过实施高校自主招生探索人才选拔制度改革,允许部分高校拿出一定比例的招生名额,选拔那些有特殊才能的学生。某学生参加一个高校的自主招生考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为 、
、 ,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试。面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为 ,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
,至少答对一题即可被录取。(假设每个环节的每个问题回答正确与否是相对独立的)
(I)求该学生被学校录取的概率;
(II)设该学生答对题目的个数为ξ,求ξ的分布列和数学期望。
(本小题满分12分)在△ABC中,内角A、B、C的对边分别为a,b,c, ,∠BAC=
,∠BAC= ,a=4.
,a=4.
(I)求bc的最大值及 的取值范围;
的取值范围;
(II)求函数 的最值
的最值
(本小题满分10分)已知关于x的不等式 .
.
(I)若 ,求不等式的解集;
,求不等式的解集;
(II)若不等式的解集为R,求实数a的取值范围。