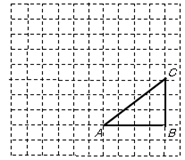
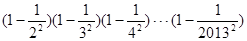如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到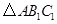 .
.
(1)在正方形网格中,作出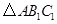 ;(不要求写作法)
;(不要求写作法)
(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留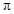 )
)
(1) 
(2)
(1)-14 -5+30-2
(2)
(3)化简:
(4)先化简,再求值: ,其中
,其中 .
.
如图,若点A在数轴上对应的数为 ,点B在数轴上对应的数为b,且
,点B在数轴上对应的数为b,且 ,b满足
,b满足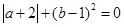
(1)求线段AB的长;
(2)点C在数轴上对应的数为x,且x是方程 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
某单位在2013 年春节准备组织部分员工到某地旅游,现在联系了甲乙两家旅行社,两家旅行社报价均为2000 元/人,两家旅行社同时都对10 人以上的团体推出了优惠措施:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队员工的费用,其余员工八折优惠.
(1)若设参加旅游的员工共有m(m>10)人,则甲旅行社的费用为元,
乙旅行社的费用为元;(用含m的代数式表示并化简)
(2)假如这个单位组织包括带队员工在内的共20名员工到某地旅游,该单位选择哪一家旅行社比较优惠?说明理由.
(3)如果这个单位计划在2月份外出旅游七天,设最中间一天的日期为n,则这七天的日期之和为 .(用含有n的代数式表示并化简)
假如这七天的日期之和为63的倍数,则他们可能于2月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程)
观察下列各式: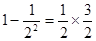 ;
;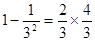 ;
; ;…;
;…;
根据上面的等式所反映的规律,
(1)填空: 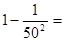 ;
; 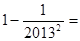 ;
;
(2)计算: