已知函数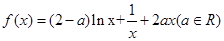 ,
,
(1)当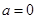 时,求
时,求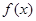 的极值;
的极值;
(2)当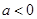 时,求
时,求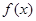 的单调区间;
的单调区间;
(3)对任意的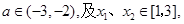 恒有
恒有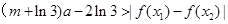 成立,求m的取值范围。
成立,求m的取值范围。
设数列 的前
的前 项和为
项和为 ,已知
,已知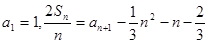 ,
,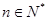 .
.
⑴求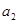 的值;
的值;
⑵求数列 的通项公式;
的通项公式;
⑶证明:对一切正整数 ,有
,有 .
.
数列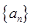 的前
的前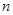 项和为
项和为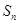 ,且满足
,且满足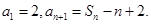
⑴求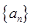 的通项公式;
的通项公式;
⑵设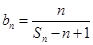 的前
的前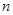 项和为
项和为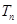 ,求
,求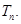
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离( -1)海里的C处的缉私船奉命以10
-1)海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.此时,走私船正以10海里/小时的速度从B向北偏西30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
海里/小时的速度追截走私船.此时,走私船正以10海里/小时的速度从B向北偏西30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
在数列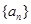 中,
中,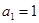 ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有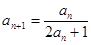 .
.
⑴证明数列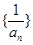 为等差数列,并求
为等差数列,并求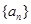 的通项公式;
的通项公式;
⑵设数列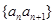 的前n项和为
的前n项和为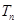 ,求使得
,求使得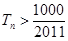 的最小正整数
的最小正整数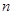 .
.
已知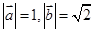 .
.
⑴若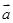 ∥
∥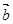 ,求
,求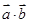 ;
;
⑵若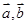 的夹角为
的夹角为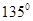 ,求
,求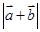 ;
;
⑶若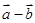 与
与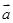 垂直,求
垂直,求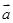 与
与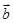 的夹角.
的夹角.