在直角坐标系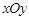 中,曲线
中,曲线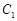 的参数方程为
的参数方程为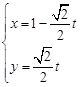 (
(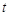 为参数),以原点
为参数),以原点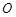 为极点,以
为极点,以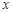 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线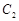 的极坐标方程为
的极坐标方程为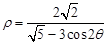 .
.
(1)求曲线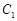 的普通方程与曲线
的普通方程与曲线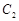 的直角坐标方程;
的直角坐标方程;
(2)曲线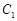 与曲线
与曲线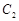 交于
交于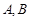 两点,
两点,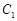 与
与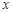 轴交于点
轴交于点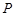 ,求
,求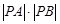 的值.
的值.
(本小题满分12分)设命题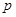 :实数
:实数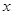 满足
满足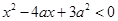 ,其中
,其中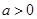 ,命题
,命题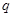 :实数
:实数 满足
满足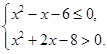 .
.
(1)若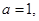 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若 是
是
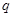 的充分不必要条件,求实数
的充分不必要条件,求实数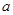 的取值范围.
的取值范围.
(本小题满分10分)选修4—5,不等式选讲
已知函数

(1)解关于 的不等式
的不等式 
(2)若函数 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。
(本小题满分10分)选修4—4:坐标系与参数方程
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,
轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4, ),若直线
),若直线 过点P,且倾斜角为
过点P,且倾斜角为 ,圆C以M为圆心,4为半径。
,圆C以M为圆心,4为半径。
(1)求直线 的参数方程和圆C的极坐标方程。
的参数方程和圆C的极坐标方程。
(2)试判定直线 与圆C的位置关系。
与圆C的位置关系。
(本小题满分10分)选修4-1:几何证明选讲
如图, 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点

(Ⅰ)证明: ∽△
∽△ ;
;
(Ⅱ)若 的面积
的面积 ,求
,求 的大小.
的大小.
(本小题满分12分)已知函数 ,其中a,b∈R,e=2.718 28 为自然对数的底数.
,其中a,b∈R,e=2.718 28 为自然对数的底数.
(1)设 是函数
是函数 的导函数,求函数g(x)在区间[0,1]上的最小值;
的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数 在区间(0,1)内有零点,求a的取值范围.
在区间(0,1)内有零点,求a的取值范围.