(本小题满分10分)选修4—5,不等式选讲
已知函数

(1)解关于 的不等式
的不等式 
(2)若函数 的图象恒在函数
的图象恒在函数 的上方,求实数
的上方,求实数 的取值范围。
的取值范围。
(本小题满分12分).已知函数f(x)=mlnx+(m-1)x(m∈R).
(1)求m=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)若f(x)存在最大值M,且M>0,求m的取值范围.
(本小题满分12分)已知圆C1:x2+y2=r2截直线x+y-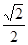 =0所得的弦长为
=0所得的弦长为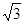 .抛物线C2:x2=2py(p>0)的焦点在圆C1上.
.抛物线C2:x2=2py(p>0)的焦点在圆C1上.
(1)求抛物线C2的方程;
(2)过点A(-1,0)的直线l与抛物线C2交于B,C两点,又分别过B、C两点作抛物线C2的切线,当两条切线互相垂直时,求直线l的方程.
(本小题满分12分)某数学老师对本校2015届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取了20名学生的成绩,分数用茎叶图记录如图:
得到频率分布如下:
| 分数段 |
[50, 70) |
[70, 90) |
[90, 110) |
[110, 130) |
[130, 150] |
总计 |
| 频数 |
b |
|||||
| 频率 |
a |
0.25 |
(1)求表中a,b的值,并估计这次考试全校学生数学成绩的及格率(分数在[90,150]范围内为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
(本小题满分12分)在四棱锥P-ABCD中,PC⊥平面ABCD,DC∥AB,DC=1,AB=4,BC=2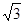 ,∠CBA=30°.
,∠CBA=30°.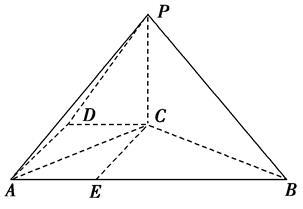
(1)求证:AC⊥PB;
(2)当PD=2时,求此四棱锥的体积.
(本小题满分12分)已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)在函数f(x)=3x2-2x的图象上.
(1)求数列{an}的通项公式;
(2)设bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.