(本小题满分12分)已知圆C1:x2+y2=r2截直线x+y-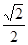 =0所得的弦长为
=0所得的弦长为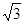 .抛物线C2:x2=2py(p>0)的焦点在圆C1上.
.抛物线C2:x2=2py(p>0)的焦点在圆C1上.
(1)求抛物线C2的方程;
(2)过点A(-1,0)的直线l与抛物线C2交于B,C两点,又分别过B、C两点作抛物线C2的切线,当两条切线互相垂直时,求直线l的方程.
(本小题满分12分)已知曲线C的极坐标方程是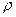 =1,以极点为原点,极轴为
=1,以极点为原点,极轴为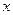 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线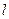 的参数方程为
的参数方程为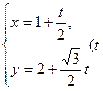 为参数)。
为参数)。
(1)写出直线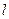 与曲线C的直角坐标方程;
与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换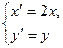 得到曲线
得到曲线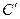 ,设曲线
,设曲线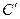 上任一点为
上任一点为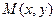 ,求
,求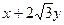 的最小值。
的最小值。
(本小题满分12分)已知函数f(x)=|x-8|-|x-4|。
(1)在答题卡相应的坐标系上作出y=f(x)的图像。
(2)解关于x的不等式f(x)>2。
(本小题满分12分)已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.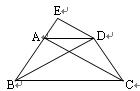
求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
(本小题满分12分) 已知圆O1和O2交于A、B两点,AC为圆O1的切线,过B作两圆的割线DE交AC于P。
(1)求证:AD//EC
(2)若AD是圆O2的切线,且PA=6,PC=2,BD=9,求AD的长。
(本小题满分12分)在直角坐标系XOY中,以O为极点,X轴正半轴为极轴建立极坐标系。曲线C的极坐标方程是: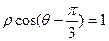 ,M,N分别是曲线C与X、Y轴的交点。
,M,N分别是曲线C与X、Y轴的交点。
(1)写出C的直角坐标系方程。并求M,N的极坐标。
(2)设MN的中点为P,求直线OP的极坐标方程。