(本小题满分13分)
已知三次函数 的导函数
的导函数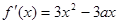 ,
, ,
, ,
,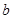 为实数。
为实数。
(1)若曲线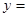
 在点(
在点(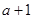 ,
, )处切线的斜率为12,求
)处切线的斜率为12,求 的值;
的值;
(2)若 在区间
在区间 上的最小值、最大值分别为
上的最小值、最大值分别为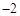 和1,且
和1,且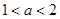 ,求函数
,求函数 的解析式。
的解析式。
(本小题满分14分)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。
(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求点C到平面A1BD的距离.
(本小题满分14分)如图,一架直升飞机的航线和山顶在同一个垂直于地面的平面内,已知飞机的高度为海拔10千米,速度为180千米/小时,飞行员先看到山顶的俯角为 ,经过2分钟后又看到山顶的俯角为
,经过2分钟后又看到山顶的俯角为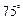 ,求山顶的海拔高度.
,求山顶的海拔高度. 
(本小题满分12分)过点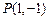 有一条直线l,它夹在两条直线
有一条直线l,它夹在两条直线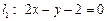 与
与 之间的线段恰被点P平分,求直线l的方程.
之间的线段恰被点P平分,求直线l的方程.
(本小题满分12分)已知函数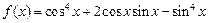 .
.
(1)求 的递减区间;
的递减区间;
(2)当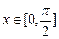 时,求
时,求 的最小值以及取得最小值时
的最小值以及取得最小值时 的集合.
的集合.
(本题12分)已知关于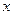 的不等式
的不等式 ,其中
,其中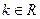 .
.
(Ⅰ)当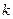 变化时,试求不等式的解集
变化时,试求不等式的解集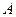 ;
;
(Ⅱ)对于不等式的解集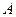 ,若满足
,若满足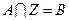 (其中
(其中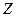 为整数集). 试探究集合
为整数集). 试探究集合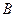 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合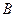 中元素个数最少的
中元素个数最少的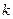 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合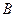 ;若不能,请说明理由.
;若不能,请说明理由.