(本小题共14分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为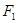 ,
, , 点
, 点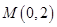 是椭圆的一个顶点,△
是椭圆的一个顶点,△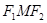 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线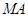 ,
, 交椭圆于
交椭圆于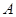 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为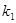 ,
,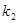 ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
求证: .
.
已知向量 ,
, .
.
(Ⅰ)求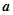 与
与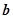 的夹角的余弦值;
的夹角的余弦值;
(Ⅱ)若向量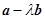 与
与 平行,求
平行,求 的值.
的值.
已知椭圆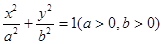 的离心率为
的离心率为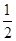 ,两焦点之间的距离为4.
,两焦点之间的距离为4.
(I)求椭圆的标准方程;
(II)过椭圆的右顶点作直线交抛物线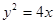 于A、B两点.
于A、B两点.
(1)求证:OA⊥OB;
(2)设OA、OB分别与椭圆相交于点D、E,过原点O作直线DE的垂线OM,垂足为M,证明|OM|为定值.
已知数列 的首项
的首项 ,前
,前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设函数 ,
, 是函数
是函数 的导函数,令
的导函数,令 ,求数列
,求数列 的通项公式,并研究其单调性.
的通项公式,并研究其单调性.
海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为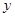 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里 处,如图.现假设:
处,如图.现假设: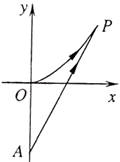
①失事船的移动路径可视为抛物线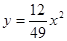 ;
;
②定位后救援船即刻沿直线匀速前往救援;
③救援船出发 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为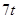 .
.
(1)当 时,写出失事船所在位置
时,写出失事船所在位置 的纵坐标.若此时两船恰好会合,求救援船速度的大小;
的纵坐标.若此时两船恰好会合,求救援船速度的大小;
(2)问救援船的时速至少是多少海里才能追上失事船?