定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:(1)如图甲,已知△ABC中∠C=90°,你能把△ABC分割成2个与它自己相似的小直角三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可将原三分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割,称为1阶分割(如图1);把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割,称为2阶分割(如图2)……依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形(n为正整数),设此时小三角形的面积为Sn.
①若△DEF的面积为1000,当n为何值时,3<Sn<4?
(请用计算器进行探索,要求至少写出二次的尝试估算过程)
②当n>1时,请写出一个反映Sn-1,Sn,Sn+1之间关系的等式(不必证明)

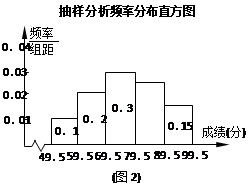
结合“两纲教育”,某中学600名学生参加了“让青春飞扬”知识竞赛.竞赛组委会从中随机抽取了部分学生的成绩(得分都是整数,最高分98分)作为样本进行统计分析,并绘制成抽样分析分类统计表和频率分布直方图(如表1和图2,部分数据缺失).试根据所提供的信息解答下列问题:
(1) 本次随机抽样调查的样本容量是 ;
(2) 试估计全校所有参赛学生中成绩等第为优良的学生人数;
(3) 若本次随机抽样的样本平均数为76.5,又表1中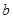 比
比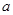 大15,试求出
大15,试求出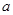 、
、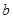 的值;
的值;
(4) 如果把满足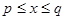 的
的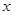 的取值范围记为[
的取值范围记为[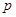 ,
,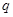 ],表1中
],表1中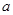 的取值范围是 .
的取值范围是 .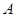 .[69.5,79.5]
.[69.5,79.5]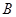 .[65,74]
.[65,74]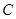 .[66.5,75.5]
.[66.5,75.5]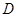 .[66,75]
.[66,75]
|
| 成绩范围 |
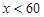 |
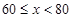 |
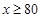 |
| 成绩等第 |
不合格 |
合格 |
优良 |
| 人数 |
40 |
||
| 平均成绩 |
57 |
a |
b |
已知⊙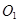 、⊙
、⊙ 外切于点
外切于点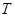 ,经过点
,经过点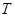 的任一直线分别与⊙
的任一直线分别与⊙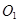 、⊙
、⊙ 交于点
交于点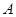 、
、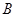 ,
,
(1)若⊙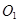 、⊙
、⊙ 是等圆(如图1),求证
是等圆(如图1),求证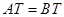 ;
;
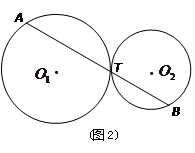
(2)若⊙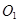 、⊙
、⊙ 的半径分别为
的半径分别为 、
、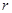 (如图2),试写出线段
(如图2),试写出线段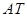 、
、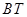 与
与 、
、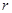 之间始终存在的数量关系(不需要证明).
之间始终存在的数量关系(不需要证明).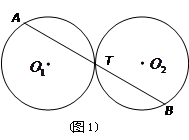
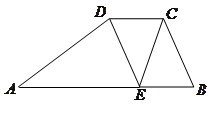
如图,已知梯形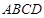 中,
中,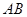 ∥
∥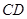 ,
,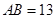 ,
,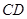 =4,点
=4,点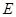 在边
在边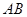 上,
上,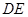 ∥
∥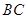 .
.
(1)若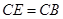 ,且
,且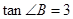 ,求
,求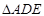 的面积;
的面积;
(2)若∠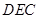 =∠
=∠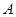 ,求边
,求边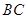 的长度.
的长度.
解方程组:

计算: .
.