如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=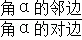 =
=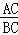 ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)ctan30°= ;
(2)如图,已知tanA=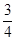 ,其中∠A为锐角,试求ctanA的值.
,其中∠A为锐角,试求ctanA的值.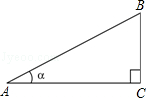
如图,已知△ABC的三个顶点在格点上.(1)作出与△ABC关于x轴对称的图形△A1B1C1;(2)求出△A1B1C1的面积.
(1)求下式中的x:9x2-4="0."
(2)计算:  .
.
(3) 求不等式的解集: 
如图,在平面直角坐标系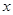 O
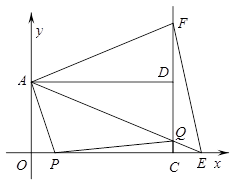
O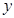 中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=
中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t秒,当t=2秒时PQ=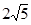 .
.
(1)求点D的坐标,并直接写出t的取值范围;
(2)连接AQ并延长交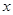 轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
如图,在平面直角坐标系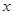 O
O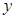 中,梯形AOBC的边OB在
中,梯形AOBC的边OB在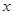 轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线
轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线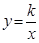 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.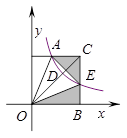
(1)填空:双曲线的另一支在第象限,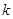 的取值范围是;
的取值范围是;
(2)若点C的坐标为(2,2),当点E 在什么位置时,阴影部分面积S最小?
(3)若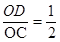 ,S△OAC="2" ,求双曲线的解析式.
,S△OAC="2" ,求双曲线的解析式.
一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.