(本小题满分12分)某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
如图,已知棱柱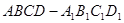 的底面是菱形,且
的底面是菱形,且 面
面 ,
,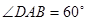 ,
,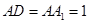 ,
,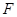 为棱
为棱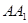 的中点,
的中点,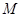 为线段
为线段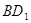 的中点,
的中点,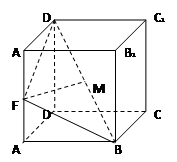
(Ⅰ)求证:  面
面 ;
;
(Ⅱ)判断直线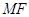 与平面
与平面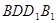 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(Ⅲ)求三棱锥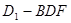 的体积.
的体积.
某大学高等数学老师这学期分别用 两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样)。现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(Ⅰ)依茎叶图判断哪个班的平均分高?
(Ⅱ)现从甲班高等数学成绩不得低于80分的同学中随机抽取两名同学,求成绩为86分的同学至少有一个被抽中的概率;
(Ⅲ)学校规定:成绩不低于85分的为优秀,请填写下面的 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关?”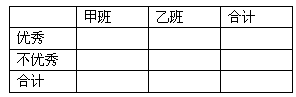
下面临界值表仅供参考:
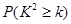 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
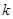 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: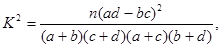 其中
其中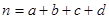 )
)
已知向量 ,
,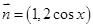 ,设函数
,设函数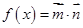 .
.
(1)求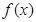 的最小正周期与单调递增区间.(2)在
的最小正周期与单调递增区间.(2)在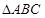 中,
中,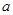 、
、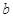 、
、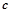 分别是角
分别是角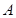 、
、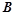 、
、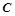 的对边,若
的对边,若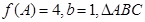 的面积为
的面积为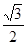 ,求
,求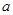 的值.
的值.
已知在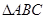 中,
中,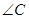 =
=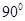 ,
,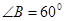 .
.
(1)过点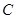 在
在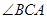 内随机的作射线
内随机的作射线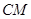 交斜边
交斜边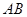 于点
于点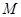 ,求
,求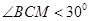 的概率;
的概率;
(2)在斜边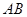 上随机的取一点
上随机的取一点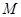 ,求
,求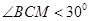 的概率.
的概率.
已知函数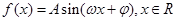 (其中
(其中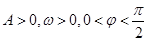 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为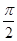 ,且图象上一个最低点为
,且图象上一个最低点为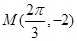 .
.
(1)求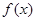 的解析式;
的解析式;
(2)当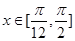 ,求
,求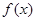 的值域.
的值域.