极坐标系的极点是直角坐标系的原点,极轴为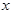 轴正半轴。已知曲线
轴正半轴。已知曲线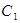 的极坐标方程为
的极坐标方程为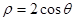 ,曲线
,曲线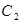 的参数方程为
的参数方程为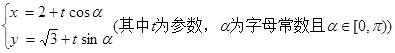
(1) 求曲线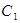 的直角坐标方程和曲线
的直角坐标方程和曲线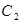 的普通方程;
的普通方程;
(2) 当曲线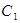 和曲线
和曲线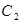 没有公共点时,求
没有公共点时,求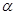 的取值范围。
的取值范围。
已知
(1)若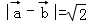 ,求证:
,求证: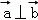
(2)设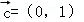 ,若
,若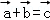 ,求α,β的值.
,求α,β的值.
如图,四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,E,F分别为棱AB,PC的中点
(1)求证:PE⊥BC;
(2)求证:EF∥平面PAD.
在△ABC中,角A,B,C所对的边分别为a,b,c,且acosB=bcosA.
(1)求证:a=b
(2)若sinA= ,求sin(C
,求sin(C )的值.
)的值.
已知函数f(x)=alnx+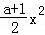 +1.
+1.
(Ⅰ)当a=﹣ 时,求f(x)在区间[
时,求f(x)在区间[ ,e]上的最值;
,e]上的最值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)当﹣1<a<0时,有f(x)>1+ ln(﹣a)恒成立,求a的取值范围.
ln(﹣a)恒成立,求a的取值范围.
已知函数f(x)=ex﹣ax﹣1(a>0,e为自然对数的底数).
(1)求函数f(x)的最小值;
(2)若f(x)≥0对任意的x∈R恒成立,求实数a的值.