(本小题满分14分)如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1. 将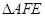 沿EF折起到
沿EF折起到 的位置,使平面
的位置,使平面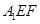 与平面BCFE垂直,连结A1B、A1P(如图2).
与平面BCFE垂直,连结A1B、A1P(如图2).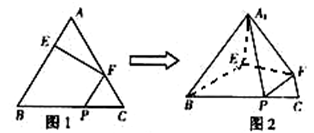
(1)求证:PF//平面A1EB;
(2)求证:平面 平面A1EB;
平面A1EB;
(3)求四棱锥A1—BPFE的体积.
据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
假设投资A项目的资金为 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利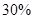 的可能性为
的可能性为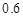 ,亏损
,亏损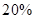 的可能性为
的可能性为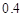 ;位于二类风区的B项目获利
;位于二类风区的B项目获利 的可能性为
的可能性为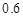 ,亏损
,亏损 的可能性是
的可能性是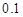 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
.
(1)记投资A,B项目的利润分别为 和
和 ,试写出随机变量
,试写出随机变量 与
与 的分布列和期望
的分布列和期望 ,
,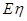 ;
;
(2)某公司计划用不超过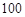 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投
资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利
润之和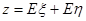 的最大值.
的最大值.
已知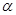 为锐角,且
为锐角,且 ,函数
,函数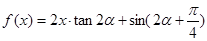 ,数列
,数列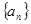 的首项
的首项 ,
,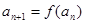 .
.
(1)求函数 的表达式;(2)求数列
的表达式;(2)求数列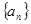 的前
的前 项和
项和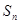 .
.
已知函数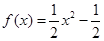 与函数
与函数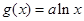 在点
在点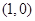 处有公共的切线,设
处有公共的切线,设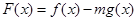
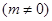 .
.
(1) 求 的值
的值
(2)求 在区间
在区间 上的最小值.
上的最小值.
已知椭圆 的焦点在
的焦点在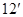 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点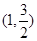 .
.
(1)求椭圆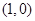 的方程;
的方程;
(2)直线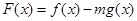 与椭圆
与椭圆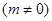 相交于
相交于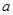 、
、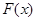 两点,
两点,  为原点,在
为原点,在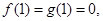 、
、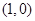 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率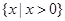 的取值范围.
的取值范围.
如图,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将 沿AF折起,得到如图所示的三棱锥
沿AF折起,得到如图所示的三棱锥 ,其中
,其中 .
.

(1) 证明: //平面
//平面 ;
;
(2) 证明:
 平面
平面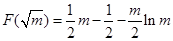 ;
;
(3)当 时,求三棱锥
时,求三棱锥 的体积
的体积