(本小题满分14分)设数列 的前
的前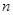 项和为
项和为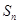 ,点
,点 在直线
在直线 上,
上, 为常数,
为常数,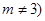 .
.
(1)求 ;
;
(2)若数列 的公比
的公比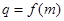 ,数列
,数列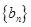 满足
满足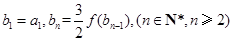 ,求证:
,求证: 为等差数列,并求
为等差数列,并求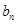 ;
;
(3)设数列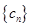 满足
满足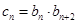 ,
,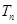 为数列
为数列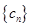 的前
的前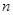 项和,且存在实数
项和,且存在实数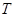 满足
满足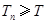 ,
, ,求
,求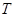 的最大值.
的最大值.
(本小题满分12分)
已知向量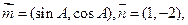 且
且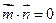 。
。
(Ⅰ)求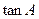 的值;
的值;
(Ⅱ)求函数 的值域。
的值域。
已知抛物线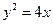 及点
及点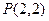 ,直线
,直线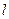 斜率为
斜率为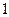 且不过点
且不过点 ,与抛物线交于点
,与抛物线交于点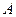 、
、 两点.
两点.
(Ⅰ)求直线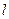 在
在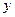 轴上截距的取值范围;
轴上截距的取值范围;
(Ⅱ)若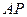 、
、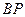 分别与抛物线交于另一点
分别与抛物线交于另一点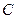 、
、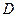 ,证明:
,证明: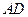 、
、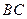 交于定点.
交于定点.
(本小题满分14分)
设函数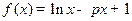
(Ⅰ)研究函数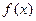 的极值点;
的极值点;
(Ⅱ)当p>0时,若对任意的x>0,恒有 ,求p的取值范围;
,求p的取值范围;
(Ⅲ)证明: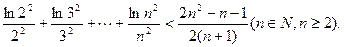
(本题满分14分)
已知函数 ,
,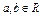 ,
,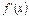 是函数
是函数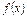 的导函数.
的导函数.
(I)若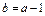 ,求函数
,求函数 的单调递减区间;
的单调递减区间;
(II)若 ,
,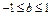 ,求方程
,求方程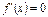 有实数根的概率.
有实数根的概率.
(本小题满分14分)
如图所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=8,AC= ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(Ⅰ)证明:PB⊥平面CEF;
(Ⅱ)求二面角B—CE—F的正弦值