如图，在△ABC中，∠C＝90º，AC＝6cm，BC＝8cm-优题课

如图，在△ABC中，∠C＝90º，AC＝6cm，BC＝8cm，D、E分别是AC、AB
的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿
BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t
＜4)s．解答下列问题：

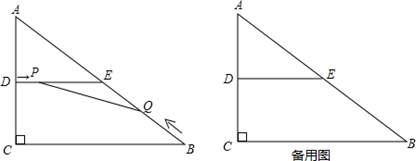
(1)当t为何值时，PQ⊥AB？
(2)当点Q在B、E之间运动时，设五边形PQBCD的面积为ycm²，求y与t之间的函数关系式；
(3)在(2)的情况下，是否存在某一时刻t，使得PQ分四边形BCDE所成的两部分的面积之比为
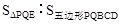＝1∶29？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．

科目数学题型解答题难度较难

知识点：相似多边形的性质

阅读下面的材料：

例1：求函数 $y = 3 x - 1$ 的反函数；

解：由 $y = 3 x - 1$ ，可得 $x = \frac{y + 1}{3}$ ，所以原函数 $y = 3 x - 1$ 的反函数是 $y = \frac{x + 1}{3}$ .

例2求函数 $y = \frac{x + 3}{x - 1} (x \neq 1)$ 的反函数.

解：由 $y = \frac{x + 3}{x - 1}$ ，可得 $x = \frac{y + 3}{y - 1}$ ，所以原函数 $y = \frac{x + 3}{x - 1}$ 的反函数是 $y = \frac{x + 3}{x - 1} (x \neq 1)$ .

以上两例中，在相应的条件下，一个原函数有反函数时，原函数中自变量 $x$ 的取值范围就是它的反函数中函数值 $y$ 的取值范围，原函数中函数值 $y$ 的取值范围就是它的反函数中自变量 $x$ 的取值范围，通过以上内容完成下面任务.

（1）求函数 $y = - 2 x + 3$ 的反函数；

（2）函数 $y = \frac{x - 2}{x + 1}$ 的反函数的函数值的取值范围为＿＿＿＿＿；

$y \neq 1$

$y \neq - 1$

$y \neq - 2$

$y \neq 2$

（3）下列函数中反函数是它本身的是＿＿＿＿＿（填序号即可）.

① $y = x$ ；② $y = x + 1$ ；③ $y = - x + 1$ ；④ $y = \frac{1}{x}$ ；⑤ $y = \frac{x + 1}{x - 1} (x \neq 1)$

某景区的旅游线路如图①，其中 $A$ 为人口， $B, C, D$ 为风景点， $E$ 为三岔路的交汇点。图①中所给数据为相应两点间的路程（单位： $km$ ）.甲游客以一定的速度沿线路“ $A \to D \to C \to E \to A$ ”步行游览，在每个景点，逗留的时间相同，当他回到 $A$ 处时，共用去 $3 h$ .甲步行的路程 $s (km)$ 与游览时间 $t (h)$ 之间的部分函数图像如图②所示.

（1）求甲在每个景点逗留的时间，并补全图像；

（2）求 $C, E$ 两点间的路程；

（3）乙游客与甲游客同时从 $A$ 处出发，打算游完三个景点后回到 $A$ 处，两人相约先到者在 $A$ 处等候，等候时间不超过 $10 min$ .如果乙的步行速度为 $3 km / h$ ，在每个景点逗留的时间与甲相同，他们的约定能否实现?请说明理由.

某单位计划派若干名员工参加电脑培训，现从两家电脑公司了解到，同样的培训条件，每名学员的培训费都报价为 $a$ 元，甲公司的优惠条件是：一名学员按报价收费，其余学员每人优惠 $25 %$ ；乙公司的优惠条件是：每名学员优惠20%.

（1）分别写出甲、乙两公司总收费 $y$ （元）关于学员人数 $x$ （人）的函数解析式；

（2）讨论该单位在哪家公司的培训总费用较低.

已知函数 $f (x) = 1 + \frac{2}{x}$ ，其中 $f (a)$ 表示 $x = a$ 时对应的函数值，即 $f (a) = 1 + \frac{2}{a}$ .

（1）求 $f (10)$ ；

（2）计算： $f (1) \cdot f (2) \cdot f (3) \cdot \dots \cdot f (100)$ 的值；

（3）如果 $f (a) - f (a + 1) = 1$ ，试求 $a$ 的值.

如图，在梯形 $ABCD$ 中， $AD / / BC, E$ 是 $BC$ 的中点， $AD = 5, BC = 12, CD = 4 \sqrt{2}, ∠ C = 45 °$ ，点 $P$ 是 $BC$ 边上一动点，设 $PB$ 的长为 $x$ .

（1）当 $x$ 的值为＿＿＿＿＿时，以点 $P, A, D, E$ 为顶点的四边形为直角梯形?

（2）当 $x$ 的值为＿＿＿＿＿时，以点 $P, A, D, E$ 为顶点的四边形为平行四边形?

（3）点 $P$ 在 $BC$ 边上运动的过程中，以 $P, A, D, E$ 为顶点的四边形能否构成菱形?试说明理由.