在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到红球的概率是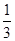 ,从袋中任意摸出2个球,至少得到一个黑球的概率是
,从袋中任意摸出2个球,至少得到一个黑球的概率是 。
。
求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。(结果用分数表示)
(本题满分16分)
已知函数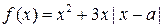 ,其中
,其中 ,
,
(1)当 时,把函数
时,把函数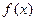 写成分段函数的形式;
写成分段函数的形式;
(2)当 时,求
时,求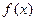 在区间
在区间 上的最值;
上的最值;
(3)设 ,函数
,函数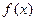 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用 表示).
表示).
(本题满分16分)
设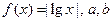 为实数,且
为实数,且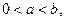
(1)求方程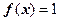 的解;
的解;
(2)若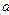 ,
,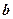 满足
满足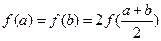 ,试写出
,试写出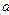 与
与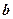 的等量关系(至少写出两个);
的等量关系(至少写出两个);
(3)在(2)的基础上,证明在这一关系中存在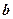 满足
满足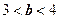 .
.
(本题满分15分)
已知定义在 上的函数
上的函数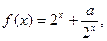
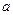 为常数,若
为常数,若 为偶函数
为偶函数
(1)求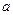 的值;
的值;
(2)判断函数 在
在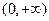 内的单调性,并用单调性定义给予证明;
内的单调性,并用单调性定义给予证明;
(3)求函数 的值域.
的值域.
(本题满分15分)
已知函数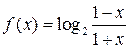 ,
,
(1)求函数的定义域;
(2)判断函数的奇偶性,并给予证明;
(3)求不等式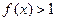 的解集.
的解集.
(本题满分14分)
化简、求值下列各式:
(1)
(2)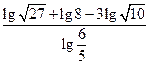 (注:
(注: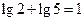 )
)