:等差数列 的各项均为正数,其前
的各项均为正数,其前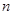 项和为
项和为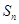 ,满足
,满足 ,且
,且 .
.
⑴求数列 的通项公式;
的通项公式;
⑵设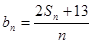 ,求数列
,求数列 的最小值项.
的最小值项.
数列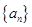 满足
满足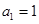 ,
,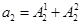 ,……,
,……,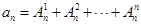 (
(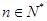 )
)
(1)求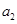 ,
,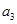 ,
,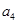 ,
,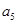 的值;
的值;
(2)求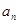 与
与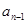 之间的关系式
之间的关系式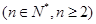 ;
;
(3)求证: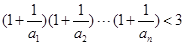 (
(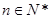 )
)
如图,椭圆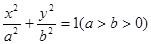 的左、右焦点为
的左、右焦点为 ,
,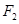 ,过
,过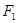 的直线
的直线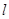 与椭圆相交于
与椭圆相交于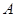 、
、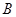 两点.
两点.
(1)若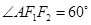 ,且
,且 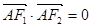 ,求椭圆的离心率.
,求椭圆的离心率.
(2)若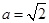 ,
,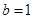 ,求
,求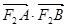 的最大值和最小值.
的最大值和最小值.
在三棱柱 中,已知
中,已知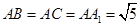 ,
, ,
,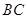 的中点为
的中点为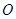 ,
,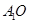 垂直于底面
垂直于底面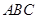 .
.
(1)证明:在侧棱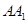 上存在一点
上存在一点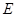 ,使得
,使得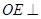 平面
平面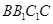 ,并求出
,并求出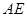 的长;
的长;
(2)求二面角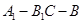 的平面角的余弦值.
的平面角的余弦值.
已知椭圆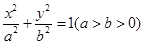 的右焦点为
的右焦点为 ,
,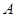 为短轴的一个端点,且
为短轴的一个端点,且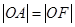 ,
,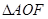 的面积为1(其中
的面积为1(其中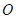 为坐标原点).
为坐标原点).
(1)求椭圆的方程;
(2)若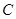 ,
,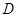 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点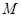 满足
满足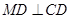 ,连接
,连接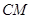 ,交椭圆于点
,交椭圆于点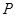 ,证明:
,证明: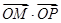 为定值.
为定值.
某班共有36名学生,其中有班干部6名,现从36名同学中任选2名代表参加某次活动,求:
(1)恰有1名班干部当选代表的概率;
(2)至少有1名班干部当选代表的概率;
(3)已知36名学生中男生比女生多,若选得同性代表的概率等于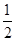 ,则男生比女生多几人?
,则男生比女生多几人?