:已知函数 .
.
(Ⅰ)若 ,令函数
,令函数 ,求函数
,求函数 在
在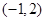 上的极大值、极小值;
上的极大值、极小值;
(Ⅱ)若函数 在
在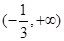 上恒为单调递增函数,求实数
上恒为单调递增函数,求实数 的取值范围.
的取值范围.
己知函数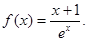
(1)求函数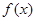 的单调区间;
的单调区间;
(2)设函数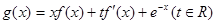 ,是否存在实数a、b、c∈[0,1],使得
,是否存在实数a、b、c∈[0,1],使得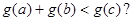 若存在,求出t的取值范围;若不存在,说明理由.
若存在,求出t的取值范围;若不存在,说明理由.
已知椭圆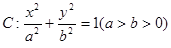 的离心率为
的离心率为 ,其左、右焦点为F1、F2,点P是坐标平面内一点,且
,其左、右焦点为F1、F2,点P是坐标平面内一点,且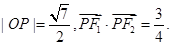 其中O为坐标原点。
其中O为坐标原点。
(I)求椭圆C的方程;
(II)如图,过点S(0,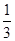 },且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
},且斜率为k的动直线l交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.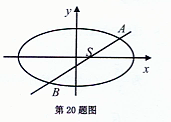
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示。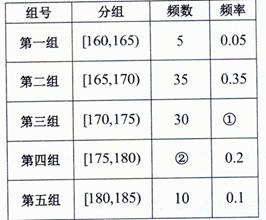
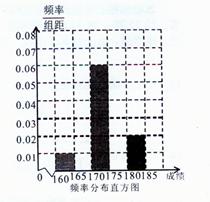
(1)请求出①②位置相应的数字,填在答题卡相应位置上,并补全频率分布直方图;
(2)为了能选出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试,求第3、4、5组中每组各抽取多少人进入第二轮的面试;假定考生“XXX”笔试成绩为178分,但不幸没入选这100人中,那这样的筛选方法对该生而言公平吗?为什么?
(3)在(2)的前提下,学校决定在12人中随机抽取3人接受“王教授”的面试,设第4组中被抽取参加“王教授”面试的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
己知函数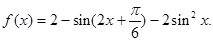
(1)求函数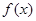 的最小正周期。
的最小正周期。
(2)记△ABC的内角A、B、C的对边长分别为a、b、c,若,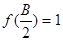 、b=1、c=
、b=1、c=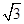 ,求a的值.
,求a的值.
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分8分.
如果存在常数 使得数列
使得数列 满足:若
满足:若 是数列
是数列 中的一项,则
中的一项,则 也是数列
也是数列 中的一项,称数列
中的一项,称数列 为“兑换数列”,常数
为“兑换数列”,常数 是它的“兑换系数”.
是它的“兑换系数”.
(1)若数列: 是“兑换系数”为
是“兑换系数”为 的“兑换数列”,求
的“兑换数列”,求 和
和 的值;
的值;
(2)已知有穷等差数列 的项数是
的项数是 ,所有项之和是
,所有项之和是 ,求证:数列
,求证:数列 是“兑换数列”,并用
是“兑换数列”,并用 和
和 表示它的“兑换系数”;
表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列 ,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.
,是否有可能它既是等比数列,又是“兑换数列”?给出你的结论并说明理由.