(本小题满分14分)
某工厂生产一种产品的成本费共由三部分组成:①原材料费每件50元;②职工工资支出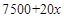 元;③电力与机器保养等费用为
元;③电力与机器保养等费用为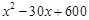 元.其中
元.其中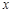 是该厂生产这种产品的总件数。
是该厂生产这种产品的总件数。
(1)把每件产品的成本费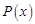 (元)表示成产品件数
(元)表示成产品件数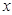 的函数,并求每件产品的最低成本费;
的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量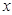 不超过170件且能全部销售,根据市场调查,每件产品的销售价为
不超过170件且能全部销售,根据市场调查,每件产品的销售价为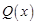 (元),且
(元),且 ,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
,试问生产多少件产品,总利润最高?并求出最高总利润。(总利润=总销售额-总的成本)
已知等差数列 的前
的前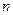 项和为
项和为 ,公差
,公差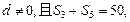
 成等比数列.
成等比数列.
(Ⅰ)求数列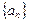 的通项公式;
的通项公式;
(Ⅱ)若从数列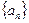 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……, ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列 ,记该数列的前
,记该数列的前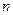 项和为
项和为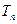 ,求
,求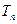 的表达式.
的表达式.
已知二次函数 (
( 为常数且
为常数且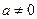 )满足条件
)满足条件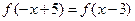 ,且方程
,且方程 有等根.
有等根.
(1)求 的解析式;
的解析式;
(2)是否存在实数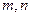 使
使 的定义域和值域分别为
的定义域和值域分别为 和
和 ?如果存在,求出
?如果存在,求出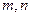 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
已知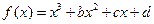 的图象过点
的图象过点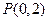 ,且在点
,且在点 处的切线方程为
处的切线方程为 .(1)求
.(1)求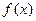 的解析式;(2)求函数
的解析式;(2)求函数 的单调区间.
的单调区间.
给出函数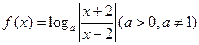 ,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=
,(1) 求函数定义域;(2)判断函数的奇偶性;(3)求使y=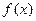 图象在
图象在 轴上方的
轴上方的 取值范围.
取值范围.
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距d(m)与车速v(km/h)和车长l(m)的关系满足: (k为正的常数),假定车身长为4m,当车速为60(km/h)时,车距为2.66个车身长。
(k为正的常数),假定车身长为4m,当车速为60(km/h)时,车距为2.66个车身长。
(1)写出车距d关于车速v的函数关系式;
(2)应规定怎样的车速,才能使大桥上每小时通过的车辆最多?