已知双曲线
,
为
上的任意点.
(1)求证:点
到双曲线
的两条渐近线的距离的乘积是一个常数;
(2)设点
的坐标为
,求
的最小值.
如图,某住宅小区的平面图呈圆心角为 的扇形 ,小区的两个出入口设置在点 及点 处,且小区里有一条平行于 的小路 ,已知某人从 沿 走到 用了10分钟,从 沿 走到 用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径 的长(精确到1米).

如图,在棱长为2的正方体 中, 是 的中点,求直线 与平面 所成角的大小(结果用反三角函数表示).

如图,已知点 在正方体 的对角线 上, .
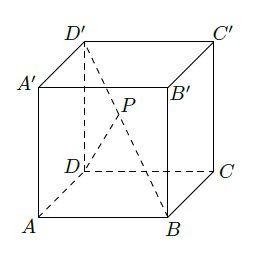
(Ⅰ)求
与
所成角的大小;
(Ⅱ)求DP与平面
所成角的大小.
已知函数
(1)若 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(2)若 ,证明:
,证明: