已知函数 ,其中
,其中 为实数.
为实数.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)是否存在实数 ,使得对任意
,使得对任意 ,
, 恒成立?若不存在,请说明理由,若存在,求出
恒成立?若不存在,请说明理由,若存在,求出 的值并加以证明.
的值并加以证明.
本题共有3个小题,第1小题满分4分,第2小题满分8分,第3小题满分6分.
已知负数 和正数
和正数 ,且对任意的正整数n,当
,且对任意的正整数n,当 ≥0时, 有[
≥0时, 有[ ,
, 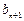 ]=
]=
[ ,
,  ];当
];当 <0时, 有[
<0时, 有[ ,
, 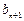 ]= [
]= [ ,
, 
 ].
].
(1)求证数列{ }是等比数列;
}是等比数列;
(2)若 ,求证
,求证
 ;
;
(3)是否存在 ,使得数列
,使得数列 为常数数列?请说明理由
为常数数列?请说明理由
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
已知函数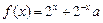 (常数
(常数 .
.
(1)若 ,且
,且 ,求x的值;
,求x的值;
(2)若 ,求证函数
,求证函数 在
在 上是增函数;
上是增函数;
(3)若存在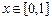 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
本题共有2个小题,第1小题满分6分,第2小题满分8分.
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是
 上一点.设
上一点.设 ,长方形PQCR的面积为S平方米.
,长方形PQCR的面积为S平方米.
(1)求S关于 的函数解析式;
的函数解析式;
(2)设 ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
( 本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
已知 ,
, ,
, 为△ABC的三个内角,向量
为△ABC的三个内角,向量 ,
, ,且
,且 .
.
(1)求 的大小;
的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.
本题共2个小题,第1小题6分,第2小题6分.
已知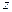 是复数,
是复数,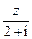 为实数(
为实数(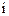 为
为 虚数单位),且
虚数单位),且 .
.
(1)求复数 ;
;
(2)若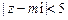 ,求实数
,求实数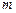 的取值范围.
的取值范围.