已知关于x的一元二次方程x2 + 2(k-1)x + k2-1 = 0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
九年级五班某同学为了测量某市电视台的高度,进行了如下操作:
(1)在点A处安置测倾器,测得塔顶C的仰角∠CAB=30°;
(2)他沿着电视塔方向前进了80米到达B处,又测得塔顶C的仰角为60°;
(3)量出测倾器AF的高度AF=1.5米.根据测量数据,请你计算出电视塔的高度CE约为多少米.(精确到0.1米, ≈1.73)
≈1.73)
已知Rt△ABC的斜边AB在平面直角坐标系的x轴上,点C(1,3)在反比例函数y= 的图象上,且sin∠BAC=
的图象上,且sin∠BAC= .
.
(1)求k的值和边AC的长;
(2)求点B的坐标.
先化简,再求值: ,其中a=-3.
,其中a=-3.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.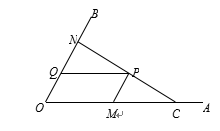
(1)若∠AOB=60º,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: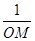 -
-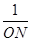 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1,△NOC的面积为S2,求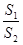 的取值范围.
的取值范围.
一次函数y= x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
x的图像如图所示,它与二次函数y=ax2-4ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.