(1) 求函数 (
( )的最大值与最小值;
)的最大值与最小值;
(2) 已知函数 (
( 是常数,且
是常数,且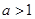 )在区间
)在区间 上有最大值
上有最大值 ,最小值
,最小值 ,
,
求实数 的值.
的值.
(本小题满分12分)
平面内动点P(x,y)与两定点A(-2, 0), B(2,0)连线的斜率之积等于 ,若点P的轨迹为曲线E,过点Q
,若点P的轨迹为曲线E,过点Q 作斜率不为零的直线
作斜率不为零的直线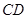 交曲线E于点
交曲线E于点 .
.
(1)求曲线E的方程;
(2)求证: ;
;
(3)求 面积的最大值.
面积的最大值.
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF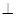 平面EFDC.
平面EFDC.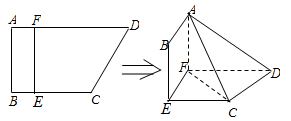
(1)当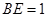 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点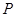 ,使得CP∥平面ABEF?若存在,求出P点位置,若不存在,说明理由;
,使得CP∥平面ABEF?若存在,求出P点位置,若不存在,说明理由;
(2)设BE=x,问当x为何值时,三棱锥A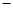 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
(本小题满分12分)在 中,已知角A、B、C所对的边分别为
中,已知角A、B、C所对的边分别为 ,直线
,直线 与直线
与直线 互相平行(其中
互相平行(其中 ).
).
(1)求角A的值;
(2)若 的取值范围.
的取值范围.
(本小题满分12分)“等比数列  中,
中, ,且
,且  是
是  和
和  的等差中项,若
的等差中项,若 
(1)求数列  的通项公式;
的通项公式;
(2)求数列 的前
的前 项和.
项和.
(不等式选讲)(本小题满分10分)设函数
(1)求不等式 的解集;
的解集;
(2)若不等式

 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.