【阅读】
在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为(,).
【运用】
⑴如图,矩形ONEF的对角线交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为______;
⑵在直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.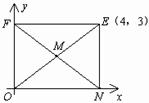
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N。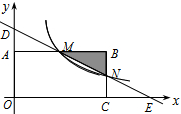
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数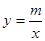 (x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数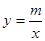 (x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
(x>0)的图象与△MNB有公共点,请直接写出m的取值范围。
如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。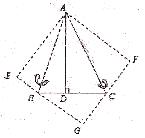
小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G点,求证:四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
如图,矩形ABCD中,P是线段AD上一动点,O为BD中点,PO的延长线交BC于Q。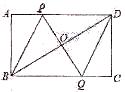
(1)求证:四边形PDQB为平行四边形;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向D运动(不与D重合)。设点P运动时间为t秒,请用t表示PD的长,并求t为何值时,四边形PBQD是菱形。
某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降1元,其销量可增加10件。
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.8m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其中,落在墙壁上的影长为1.5m,落在地面上的影长为4.8m,求树的高为多少米?